Hallo kati.99 !
1. Maximum oder Minimum
\( M_{1}=\left\{n \in \mathbb{N} \mid n^{2}<18;\ {\color{blue}0\notin \mathbb{N}}\right\}\\ M_{2}=\{x \in \mathbb{R}\ |\ | x-1 \mid \leq 2\}\\ M_{3}=\{x \in \mathbb{R} \mid 0 \} \\ {\color{blue}{Keine\ Extrema\ in\ \{M_1;\ M_2;\ M_3\}.}\ \color{red}\ Leider\ nicht\ korrekt.}\)
siehe unten.
2. Welche der folgenden Mengen sind induktiv?
\(\begin{array}{l} A=\{x \in \mathbb{R} \mid x \geq-3\}, \quad B=\left\{n+\frac{1}{2} \mid n \in \mathbb{N}\right\}, \quad C=\{2 n+1 \mid n \in \mathbb{N}\}, \\ D=\{2 n-1 \mid n \in \mathbb{N}\}, \quad E=\{x \in \mathbb{R} \mid x>1\}, \quad F=\left\{n \in \mathbb{N} \mid n^{2}<18\right\} \end{array}\)
Zur Beantwortung dieser Frage reicht mein Wissen nicht aus. Du kannst dich hier informieren:
https://de.wikipedia.org/wiki/Induktive_Menge
![]() !
!
Naja, Wiki zB. sieht das Euler-Produkt nur in Zusammenhang mit multiplikativen zahlentheoretischen Funktionen und den zugehörigen Dirichlet-Reihen:
https://de.wikipedia.org/wiki/Euler-Produkt
Du betrachtest dann quasi einen Spezialfall von der Wiki-Definition mit f = 1.
Du bist also auf der Suche nach dem Wert von \(\Pi_f \frac{1}{1-f^{-s}}\) (das f eigentlich unterm Pi) (wobei f die Fibonacci-Folge ist)?
Mit den Fibonacci-Zahlen ergibt sich hier auf jeden Fall das Problem, dass der Nenner für die ersten beiden Fibonacci-Zahlen Null wird. Bei den Primzahlen ist das nicht der Fall, denn 1 ist nicht prim. Für das "neue Euler-Produkt" müssen wir also die ersten beiden Zahlen auslassen damit das Produkt überhaupt definiert ist.
Bevor wir da jetzt tiefer einsteigen kann ich schonmal den Hinweis da lassen, dass du dir mit Excel (oder dem OpenOffice-Abklatsch davon oÄ.) bequem so viele Werte anschauen kannst wie du willst. Habs dir mal vorgemacht (incl. benutzter Formeln), sieht dann so aus:
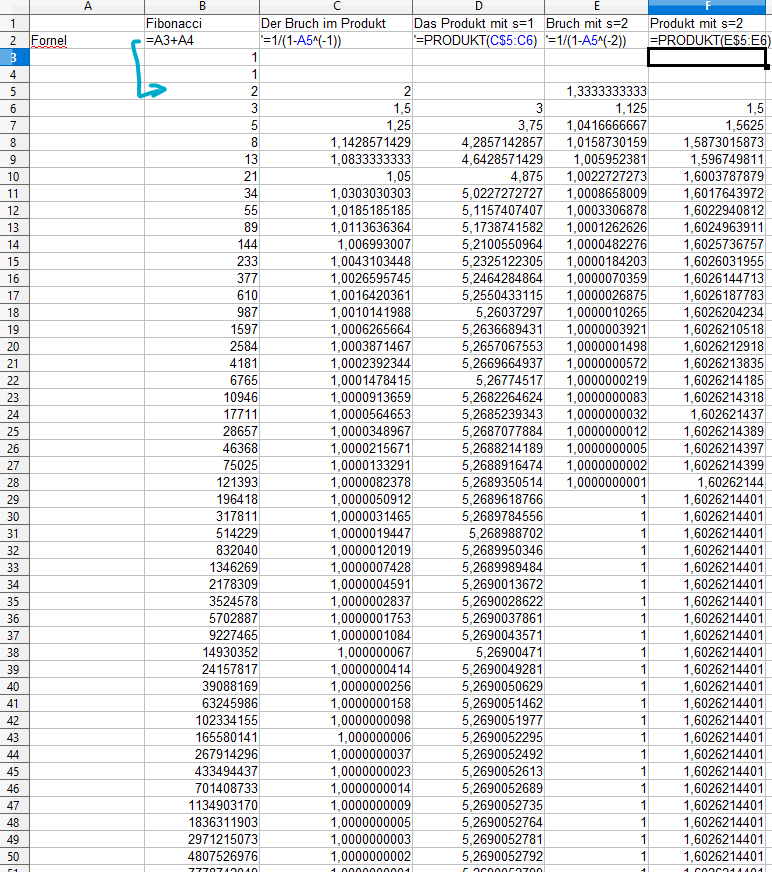
Insbesondere sieht's aus, als würde das auch für s=1 konvergieren.
Nummerierung nach https://de.wikipedia.org/wiki/Peano-Axiome .
(1) ist nicht erfüllt - gibt ja keine Null.
(2) und (3) sind auch erfüllt - warum ist vermutlich klar, die Aussagen passen zur angegebenen Nachfolgerfunktion.
(4) ist das erste, das nicht erfüllt ist. 1 und 3 sind zwei unterschiedliche Zahlen, die aber den gleichen Nachfolger haben.
(5) ist technisch gesehen korrekt, da aufgrund des Nicht-Vorhanden-Seins der 0 die linke Seite des Folgepfeils stets unwahr ist.
Vermutlich hast du eine Version der Peano-Axiome vorliegen, wo noch 1 statt 0 benutzt wird. Dann sieht's so aus:
(1) offenbar wahr. (2) auch.
(3) nicht wahr: 1 ist der Nachfolger von 2.
(4) aus den gleichen Gründen wie oben nicht erfüllt
(5) auch nicht erfüllt: Eine Menge könnte, obwohl die linke Seite des Folgepfeils erfüllt ist (also 1 enthalten und jeder Nachfolger), nur 1 und 2 enthalten. Daher wäre nicht die ganze Menge N enthalten.
Was gemeint ist ist wohl 125=53. Die Zahlen davor sind 13, 23 etc.
Generell lässt sich aber jede Zahl als Lösung rechtfertigen. Man "rät" ja quasi, was sich der, der die Formel geschrieben hat, dabei gedacht hat. Es könnten auch die Geburtsjahre seiner Lieblingspersönlichkeiten im 19.Jahrhundert sein, who knows.
Auch auf mathematische Art lassen sich alle Lösungen rechtfertigen. Wie das geht (mit Methoden aus der 8. Klasse tatsächlich) zeige ich in meiner Antwort hier:
https://web2.0rechner.de/fragen/mathe-frage-die-nur-menschen-mit-einen-iq-von-150