+15147 Hallo anonynymous!
Der Elastizitätsmodul von Stahl ist
E = 210 kN/mm²
Bei ideal linear elastischem Werkstoffgesetz (Proportionalitätsbereich im Spannungs-Dehnungs-Diagramm) ergibt sich die Federkonstante c eines geraden Stabes aus seiner Querschnittsfläche A, seiner Länge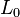 
und seinem Elastizitätsmodul E.
Mit den Ausdrücken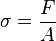 
für die Spannung und 
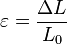für die Dehnung erhält man aus obiger Gleichung das Hookesche Gesetz für den einachsigen Spannungszustand
und daraus den E-Modul
1. A = d²*pi/4 = 0,1²mm²*pi/4
Der Querschnitt
A = (7,854 / 10³)mm²
2. σ = F/A = (5kg * 9,81m/s²)/(7,854mm²/10³)
Die Spannung
σ = 6245,225 N/mm²
3. ε = σ/E = (6245,225 N/mm²)/(210*10³ N/mm²)
Die Dehnung
ε = 0,02974
4. ΔL = L(0) * ε = 1 500mm * 0,02974
Die Längenänderung (theoretisch, weil der Draht vorher reißt)
(ΔL = 44,6mm )
5. Baustahl St37 hat eine Zugfestigkeit von σ(Br) = 37kp/mm² = 363N/mm²
F(Br) = σ(Br) * A = (363N/mm²)*(7,854/10³)mm²
Die notwendige Kraft zum Zerreißen des Drahtes aus St37 ist
Bei m = 2,851N / 9,81m/s² = 0,291kg angehängter Masse reißt der Draht.
Vielen Dank für Ihren Hinweis auf meinen Fehler Omi67! 
Gruß asinus :- )
+14538 $${\mathtt{d}} = {\mathtt{2}}{\mathtt{\,\times\,}}{\mathtt{r}}$$ $${\mathtt{U}} = {\mathtt{d}}{\mathtt{\,\times\,}}{\mathtt{\pi}}$$ $${\mathtt{A}} = {{\mathtt{r}}}^{{\mathtt{2}}}{\mathtt{\,\times\,}}{\mathtt{\pi}}$$
!+14538 $${\mathtt{c}} = {\frac{{\mathtt{2}}{\mathtt{\,\times\,}}{\mathtt{V}}}{\left({\mathtt{a}}{\mathtt{\,\times\,}}{\mathtt{b}}\right)}}$$
!
in einem video ist dieses ergebnis rausgekommen. KAnfang ist das Kapital- Kverzinst die Zinsen die man bekommt und P= Zinssatz
