Alle Antworten 24986 Antworten

Wie kann ich den Flächeninhalt eines Kreises ausrechnen?

$A=\pi \times r^2$

oder

$A=d^2\times \frac{\pi}{4}$

oder

$A=(\frac{d}{2})^2 \times \pi$

  !

Punkt vor Strich stimmt schon, es wird auch nirgendwo dagegen verstoßen. 

Das wichtige beim Umformen von Gleichungen ist, dass die Rechenoperation immer auf beiden Seiten durchgeführt wird. 

Wenn zunächst durch 1/2 geteilt werden soll, ist das ok. Dabei muss dann allerdings nicht nur 1/2x und 5/6, sondern auch 1/3 auf der linken Seite durch 1/2 geteilt werden (Jeder Summand halt ;) )

Du dividierst durch 100, um 1 Prozent zu berechnen. Dann multiplizierst du mit 2, um 2 Prozent zu erhalten. Wenn's schon etwas schneller geht, kannst du auch mit 0,02 multiplizieren.

Es geht auch kürzer.

2 * pi * Radius

Vielen dank für die Lösung.

Ich dachte ich müßte auch hier Punkt vor Strichrechnung machen, deshalb habe ich erst die 5/6:1/2 gerechnet und dann erst minus 1/3.

Gilt hier bei Gleichungen immer erst Strichrechnung und danach erst Punktrechung?

Ich habe meine Mathe-Zeit schon lange hinter mir gelassen und versuche gerade meinen Kids etwas unter die Arme zu greifen, aber alles weiß ich auch nicht mehr...

Direkt in Schritt 1 machst du quasi zwei Rechenschritte auf einmal, vergisst dabei dass du zunächst 1/3 nach rechts bringst und dann alles durch 1/2 teilst, auch 1/3.

${1 \over 2} \cdot x +{1 \over 3} = {5 \over 6} \ \ \ \ | -{1 \over 3} \\ {1 \over 2} \cdot x = {5 \over 6} - {1 \over 3} \ \ \ \ |:{1 \over 2} \\ x = { {5 \over 6} - {1 \over 3} \over {1 \over 2} }\\ = {5 \over 6 }: {1 \over 2} - {1 \over 3}:{1 \over 2} \\ = {5 \over 6} \cdot {2 \over 1} - {1\over3} \cdot {2 \over 1} \\ = {5 \over 3} - {2 \over 3} = {3\over 3} = 1$

Ich hoffe, das war nachvollziehbar.

Kann die Gleichung jemand nach F1 auflösen ?

a*ln(f1)+b*ln((f1*w1)/(a*w2)*b)=x

$\begin{array}{|rcll|} \hline a\cdot \ln(f_1)+b\cdot \ln \Big( \frac{f_1\cdot w_1} {a\cdot w_2} \cdot b \Big) &=& x \\ a\cdot \ln(f_1)+b\cdot \ln \Big( f_1 \cdot \frac{b\cdot w_1} {a\cdot w_2} \Big) &=& x \\ a\cdot \ln(f_1)+b\cdot \Big[ \ln( f_1 ) + \ln \Big( \frac{b\cdot w_1} {a\cdot w_2} \Big) \Big] &=& x \\ a\cdot \ln(f_1)+b\cdot \ln( f_1 ) + b\cdot \ln \Big( \frac{b\cdot w_1} {a\cdot w_2} \Big) &=& x \\ (a+b) \cdot \ln(f_1) + b\cdot \ln \Big( \frac{b\cdot w_1} {a\cdot w_2} \Big) &=& x \quad & | \quad - b\cdot \ln \Big( \frac{b\cdot w_1} {a\cdot w_2} \Big) \\ (a+b) \cdot \ln(f_1) &=& x - b\cdot \ln \Big( \frac{b\cdot w_1} {a\cdot w_2} \Big) \quad & | \quad : (a+b) \\ \ln(f_1) &=& \dfrac{ x - b\cdot \ln \Big( \frac{b\cdot w_1} {a\cdot w_2} \Big) } {a+b} \\ e^{\ln(f_1)} &=& e^{\Big( \dfrac{ x - b\cdot \ln ( \frac{b\cdot w_1} {a\cdot w_2} ) } {a+b} \Big) } \\ \mathbf{ f_1 } & \mathbf{=} & \mathbf{ e^{\Big( \dfrac{ x - b\cdot \ln ( \frac{b\cdot w_1} {a\cdot w_2} ) } {a+b} \Big) } } \\ \hline \end{array}$

Omi67 du bist die beste!Ich bedanke mich recht herzlich. Du hast mir praktisch den A***h gerettet. Fühl dich auf ein Bier o.ä. eingelade;-).......

Hier kommt erst mal die Lösung für Aufgabe a)

Der Rest kommt später.

wenn ich ein Lampen System habe mit drei Lampen die gerade alle aus sind

wie viele mögliche Stellungen kann ich dann einstellen

in dem ich Lampen an und oder aus mache?

$\begin{array}{|r|r|r|r|} \hline & \text{Lampe } 1 & \text{Lampe } 2 & \text{Lampe } 3 \\ \hline 1 & \color{red}{\text{aus}} & \color{red}{\text{aus}}& \color{red}{\text{aus}} \\ 2 & \color{red}{\text{aus}} & \color{red}{\text{aus}} & \color{green}{\text{an}} \\ 3 & \color{red}{\text{aus}} & \color{green}{\text{an}} & \color{red}{\text{aus}} \\ 4 & \color{red}{\text{aus}} & \color{green}{\text{an}} & \color{green}{\text{an}} \\ 5 & \color{green}{\text{an}} & \color{red}{\text{aus}} & \color{red}{\text{aus}} \\ 6 & \color{green}{\text{an}} & \color{red}{\text{aus}} & \color{green}{\text{an}} \\ 7 & \color{green}{\text{an}} & \color{green}{\text{an}} & \color{red}{\text{aus}} \\ 8 & \color{green}{\text{an}} & \color{green}{\text{an}} & \color{green}{\text{an}} \\ \hline \end{array}$

$x ^ {0.5} + x^2 = 17\\ x ^ {0.5} + (x ^ {0.5} )^4 = 17\\ let\;\;t=x ^ {0.5} \\ t+t^4=17\\ t^4+t-17=0$

This has at most 4 real answers.

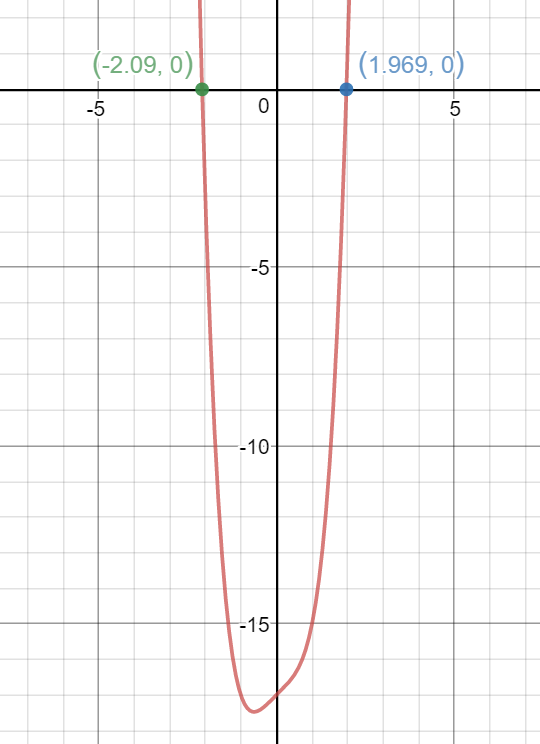
If I graph $y=x^4+x-17$

and see where it crosses the x axis that will be the solutions.

So t might equal 1.969   or   -2.09

$t=x^{0.5}\\ t^2=x\\ If\;\;t=1.969,\quad x=3.877\\ LHS=3.877^{0.5}+3.877^2=21.2\ne RHS\\~ \\If\;\;t=-2.09,\quad x=4.368\\ LHS=4.368^{0.5}+4.368^2=17=RHS\\~$

So I get   x= 3.877      Correct to 3 decimal places

I am going to enter this into WolframAlpha to see if our answers are the same.

So würde man auch dadrauf kommen:

    $\frac{5}{3} -\frac{1}{2}$

= $\frac{10}{6} - \frac{3}{6}$

= $\frac{7}{6}$ = $1 \frac{1}{6}$

Sqrt (4 ^ 5, 3) * sqrt (4 ^ 2, 5) = sqrt (15 ^ 31.15)

First I just used the web2 calc and yo ucan see they are very different.

Sqrt (4 ^ 5, 3) * sqrt (4 ^ 2, 5) = 17.5491996751140154

sqrt (15 ^ 31.15) = 2077884291032316842.5644918698908105

$\sqrt [3]{4^5}*\sqrt[5]{4^2}\\ =4^{5/3}\;\;*\;\;4^{2/5}\\ =4^{25/15}\;\;*\;\;4^{6/15}\\ =4^{(25+6)/15}\\ =4^{(30/15+1/15)}\\\\ =4^{(31/15)}\qquad \text{as guest said :)}\\ or\\ =4^{(30/15)}*4^{(1/15)}\\ =16*4^{(1/15)}\\ =16*\sqrt[15]{4}\\ $

$\begin{align} \sqrt[3]{4^5}\cdot \sqrt[5]{4^2} &= 17,549\\ \sqrt[15]{15^{31}} &= 269,518 \end{align}$

Das ist offensichtlich nicht das Gleiche.

Was du zum Beispiel machen kannst, falls du das willst/sollst:

$(\sqrt[3]{4})^5 \cdot (\sqrt[5]{4})^2=17,549$

$tan^{-1}(0.87)=\frac{1}{tan(0.87)}=\frac{1}{1.18532..}=0.8465..$

47-12hoch10 mal geteilt durch 7 ?

$\frac{47-12^{10}}{7}=-8845337739\frac{4}{7}$

$47-\frac{12^{10}}{7}=-8845337699\frac{2}{7}$

  !

fünfdrittel - einhalb ist gleich?

$\frac{5}{3}-\frac{1}{2}$

$=\frac{5\cdot2}{3\cdot2}-\frac{1\cdot3}{3\cdot2}$

$=\frac{10-3}{6}$

$=\frac{7}{6}$

  !

Was? 

(a+b)²=(a+b)*(a+b)=a²+ab+ab+b²=a²+2ab+b²

1. binomische Formel

    (a+b)² = a²+2ab+b²

Thanks Heureka,

Or maybe just 

$If\\ tan \theta = 0.87\\ then\\ \theta = tan^{-1}(0.87)\\\text{Which can also be written as }\\\theta=atan(0.87)\\ $

atan(0.87) = 0.715991114416