Hallo anonymous!
Die innere Energie einer Gasmasse betrage U1 = 3645 bar*dm3. Bei Erwärmung erhöht sich der Betrag auf U2 = 4622 bar*dm3. Welchen Raum würde das Gas jeweils unter dem Druck 1000 mbar ausfüllen?
Ich setze bei der Expansion zu p = 1000 mbar isotherme Zustandsänderung voraus.
Bei einer isothermen Zustandsänderung (T = konst.) ändert sich die innere Energie nicht.
U = pV
V1 = U1 / p
V2 = U2 / p
p = 1000 mbar = 1 bar
Dann wäre
V1 = 3645 bar * dm³ / 1 bar = 3645 dm³
V2 = 4622 bar * dm³ / 1 bar = 4622 dm³
Kommt mir, zugegeben, etwas zu einfach vor. Scheint aber richtig zu sein.
Gruß :- )
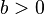 ist
ist  . Für
. Für  ist
ist  nicht definiert.
nicht definiert. , für
, für  . Der Ausdruck
. Der Ausdruck  wird entweder undefiniert gelassen oder – sofern dies zweckmäßiger ist – als 1 definiert. Siehe Potenz.
wird entweder undefiniert gelassen oder – sofern dies zweckmäßiger ist – als 1 definiert. Siehe Potenz.