Berechnen Sie alle komplexen Lösungen der folgenden Gleichung: z^2=-1+j {z=-sqrt(j-1), z=sqrt(j-1)} ist als Lösung nicht richtig meint der Lehrer es ist zu einfach. Wie mache ich das sonst noch ?
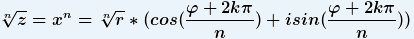k = 0,1,2, ... , n-1
$$\boxed{\ z = a+b\cdot i \qquad r = \sqrt{a^2+b^2}\ }\\\\
z^2= -1 +j \qquad a = -1 \text{ und } b = 1 \qquad r = \sqrt{(-1^2)+1^2} \quad r = \sqrt{2}\\\\
\small{\text{Wir erhalten f\"ur den Betrag $ r = \sqrt{2} $}}\\\\
\boxed{
\sqrt{z}=\sqrt{\sqrt{2}}\cdot \left(
\cos( \frac{\varphi+2k\pi } {2}) + i \cdot \sin( \frac{\varphi+2k\pi }{2} )
\right) \quad k = 0,1
}$$
$$\boxed{\ \varphi = arg(z) = \arctan{(\frac{b}{a})}\ } \qquad \varphi = \arctan{(\frac{1}{-1})} = -\frac{\pi}{4} = \frac{3}{4}\cdot \pi\\\\
\small{\text{1. L\"osung ( k=0 ):}}\\
\sqrt{z} = \sqrt{r}\left[
\cos( \frac{\varphi}{2}) + i\cdot \sin ({\frac{\varphi}{2}) }
\right]\\\\
\sqrt{z} = \sqrt{\sqrt{2} }\left[
\cos( \frac{\frac{3}{4}\cdot \pi}{2}) + i\cdot \sin ({\frac{\frac{3}{4}\cdot \pi}{2}) }
\right]\\\\
\sqrt{z} = \sqrt{\sqrt{2} }\left[
\cos( \frac{3}{8}\cdot \pi}) + i\cdot \sin ({\frac{3}{8}\cdot \pi}) }
\right]\\\\
\boxed{\sqrt{z} = 0.45508986 + i\cdot 1.098684113}$$
$$\small{\text{2. L\"osung ( k=1 ):}}\\
\sqrt{z} = \sqrt{r}\left[
\cos( \frac{\varphi+2\pi}{2}) + i\cdot \sin ({\frac{\varphi+2\pi}{2}) }
\right]\\\\
\sqrt{z} = \sqrt{\sqrt{2} }\left[
\cos( \frac{\frac{3}{4}\cdot \pi+2\pi}{2}) + i\cdot \sin ({\frac{\frac{3}{4}\cdot \pi+2\pi}{2}) }
\right]\\\\
\sqrt{z} = \sqrt{\sqrt{2} }\left[
\cos( \frac{11}{8}\cdot \pi}) + i\cdot \sin ({\frac{11}{8}\cdot \pi}) }
\right]\\\\
\boxed{\sqrt{z} = -0.45508986 - i\cdot 1.098684113}$$
.
Was muss ich der Reihe nach machen.Ich bekomme das mit dem Link nicht hin. Bei mir erscheint nur der Taschenrechner und nicht die Aufgabe.
!
