wie berechnet man die masse eines Baumstammes,
durchmesser: 12 dm
länge:3,50 m
dichte: 400 kg/kubikmeter
$$\small{\text{
$
\boxed{ \rho = \dfrac{m}{V}
\qquad m = \rho \cdot V
\qquad \rho $ ist die Dichte $\qquad V $ ist das Volumen
}
$
}}$$
$$\small{\text{
$
\boxed{ V = \pi \cdot {r^2} \cdot h \qquad
$ Gerader Zylinder mit Radius $r$ und H\"ohe $h$:
}
$
}}\\$$
$$\small{\text{
$r = \frac{d}{2} = \frac{12\ dm}{2} = 6\ dm = 0,6\ m
$}}\\
\small{\text{
$h = 3,5\ m
$}}\\\\
\small{\text{
$ V = \pi \cdot {0.6^2\ m^2} \cdot 3.5\ m \\
$}}\\
\small{\text{
$ V = \pi \cdot {0,6^2} \cdot 3,5\ m^3 \\
$}}\\
\small{\text{
$ = \pi \cdot 0,36 \cdot 3,5\ m^3
$}}\\
\small{\text{
$ = 1,26 \cdot\pi \ m^3
$}}\\
\small{\text{
$
\boxed{
V = 3,95840674352 \ m^3
}
$
}}\\\\
\small{\text{
$
m = 400 \cdot \dfrac{\ kg}{\ m^3} \cdot V
$
}}\\\\
\small{\text{
$
m = 400 \cdot \dfrac{\ kg}{\ m^3} \cdot 3,95840674352 \ m^3
$
}}\\\\
\small{\text{
$
m = 400 \cdot 3,95840674352 \cdot \dfrac{\ kg\cdot \ m^3}{\ m^3}
$
}}\\\\
\small{\text{
$
m = 400 \cdot 3,95840674352 \cdot \dfrac{\ kg\cdot \ \not{m^3}}{\ \not{m^3}}
$
}}\\\\
\small{\text{
$
m = 400 \cdot 3,95840674352 \cdot \ kg
$
}}\\
\small{\text{
$
\boxed{
m = 1583,363 \ kg
}
$
}}\\$$
Siehe auch: http://www.leifiphysik.de/themenbereiche/masse-volumen-und-dichte
![]()
![\[\binom40+\binom51+\binom62+\binom73.\]](http://latex.artofproblemsolving.com/7/9/5/795a2052ed61fcd4347921923c619886a496ad9a.png)
| If a diagonal of numbers of any length is selected starting at any of the 1's bordering the sides of the triangle and ending on any number inside the triangle on that diagonal, the sum of the numbers inside the selection is equal to the number below the end of the selection that is not on the same diagonal itself. If you don't understand that, look at the drawing. 1+6+21+56 = 84 1+7+28+84+210+462+924 = 1716 1+12 = 13 | 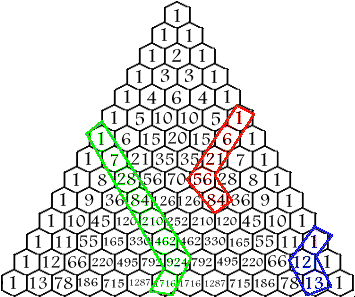 |
$$\small{\text{$\left( \begin{array}{c}4 \\ 0 \end{array} \right)$}}
+\small{\text{$\left( \begin{array}{c}5 \\ 1 \end{array} \right)$}}
+\small{\text{$\left( \begin{array}{c}6 \\ 2 \end{array} \right)$}}
+\small{\text{$\left( \begin{array}{c}7 \\ 3 \end{array} \right)$}}
=\small{\text{$\left( \begin{array}{c}8 \\ 3 \end{array} \right)$}}\\\\
\small{\text{
$\left( \begin{array}{c}8 \\ 3 \end{array} \right)
=\dfrac{8!}{3!\cdot 5!}
= \dfrac{\not{5!}\cdot 6 \cdot 7 \cdot 8 }{3!\cdot \not{5!}}
= \dfrac{6 \cdot 7 \cdot 8 }{3!}
= \dfrac{6 \cdot 7 \cdot 8 }{2\cdot 3}
=\dfrac{ 6 } { 3 }\cdot 7 \cdot \dfrac{ 8 } { 2 }
= 2\cdot 7 \cdot 4 \\
= 56
$}}$$
![]()