heureka

$$\boxed{ g=\dfrac{m \cdot G}{r^2} }$$

$$\\\small{\text{$g_{earth}=G*\dfrac{m_{earth}}{r_{earth}^2}\qquad G= 6.673 * 10^{-11} * \frac { N*\ m^2 } { kg^2 } \qquad m_{earth}=5.972\cdot 10^{24}\ kg\qquad r_{earth}=6.371\cdot 10^6\ m$}}\\\\ \small{\text{$g_{earth}=6.673 \cdot 10^{-11}*\dfrac{ 5.972\cdot 10^{24} }{ ( 6.371\cdot 10^6 )^2}\cdot \frac{N\cdot \ m^2 \cdot\ kg}{ kg^2\cdot\ m^2 } = \dfrac{ 6.673\cdot 5.972\cdot 10^{-11+24-12}} { 6.371^2 } \cdot \frac { N } { kg } $}}\\\\ \small{\text{$g_{earth}= \dfrac{ 6.673\cdot 5.972\cdot 10^{1}} { 6.371^2 } \cdot \frac { \dfrac{kg\cdot \ m }{s^2} } { kg } $}}\\\\ \small{\text{$g_{earth}= 9.81806072145\cdot \dfrac{ m }{s^2}$}}$$

There are some counters in a bag 5 red 6 blue and 1 green. Work out the probability that Jim picks out a counter that is not red ?

$$\textcolor[rgb]{150,0,0}{ 5 ~ \rm{red} } ~ bags +\textcolor[rgb]{0,0,150}{ 6 ~ \rm{blue} } ~ bags +\textcolor[rgb]{0,150,0}{ 1 ~ \rm{green} } ~ bag = 12 ~ bags$$

The probability that Jim picks out a counter that is not red is:

$$\small{\text{$ \begin{array}{l} \dfrac { \begin{pmatrix} \textcolor[rgb]{150,0,0}{r} \\ 0 \end{pmatrix}\cdot \begin{pmatrix} \textcolor[rgb]{0,0,150}{b} \\ 1 \end{pmatrix}\cdot \begin{pmatrix} \textcolor[rgb]{0,150,0}{g} \\ 0 \end{pmatrix} + \begin{pmatrix} \textcolor[rgb]{150,0,0}{r} \\ 0 \end{pmatrix}\cdot \begin{pmatrix} \textcolor[rgb]{0,0,150}{b} \\ 0 \end{pmatrix}\cdot \begin{pmatrix} \textcolor[rgb]{0,150,0}{g} \\ 1 \end{pmatrix}} { \begin{pmatrix} \textcolor[rgb]{150,0,0}{r}+ \textcolor[rgb]{0,0,150}{b}+ \textcolor[rgb]{0,150,0}{g} \\ 1 \end{pmatrix} }\\\\ = \dfrac { 1 \cdot \begin{pmatrix} \textcolor[rgb]{0,0,150}{b} \\ 1 \end{pmatrix}\cdot 1 + 1 \cdot 1 \cdot \begin{pmatrix} \textcolor[rgb]{0,150,0}{g} \\ 1 \end{pmatrix}} { \begin{pmatrix} \textcolor[rgb]{150,0,0}{r}+ \textcolor[rgb]{0,0,150}{b}+ \textcolor[rgb]{0,150,0}{g} \\ 1 \end{pmatrix} }\\\\ = \dfrac { \begin{pmatrix} \textcolor[rgb]{0,0,150}{b} \\ 1 \end{pmatrix}+ \begin{pmatrix} \textcolor[rgb]{0,150,0}{g} \\ 1 \end{pmatrix} } { \begin{pmatrix} \textcolor[rgb]{150,0,0}{r}+ \textcolor[rgb]{0,0,150}{b}+ \textcolor[rgb]{0,150,0}{g} \\ 1 \end{pmatrix} }\\\\ = \dfrac{ \textcolor[rgb]{0,0,150}{b}+ \textcolor[rgb]{0,150,0}{g} }{ \textcolor[rgb]{150,0,0}{r}+ \textcolor[rgb]{0,0,150}{b}+ \textcolor[rgb]{0,150,0}{g} } \\\\ = \dfrac{ \textcolor[rgb]{0,0,150}{6}+ \textcolor[rgb]{0,150,0}{1} }{ \textcolor[rgb]{150,0,0}{5}+ \textcolor[rgb]{0,0,150}{6}+ \textcolor[rgb]{0,150,0}{1} } \\\\ = \dfrac{ 7 }{ 12 } \end{array} $}}$$

$$\mathbf{12\binom{3}{3} + 11\binom{4}{3} + 10\binom{5}{3} + \cdots + 2\binom{13}{3} +\binom{14}{3} = \;?}$$

$$\small{\text{$ \begin{array}{l} \mathbf{ 12\binom{3}{3} + 11\binom{4}{3} + 10\binom{5}{3} + 9\binom{6}{3} + 8\binom{7}{3} + 7\binom{8}{3} + 6\binom{9}{3} + 5\binom{10}{3} + 4\binom{11}{3} + 3\binom{12}{3} + 2\binom{13}{3} + 1\binom{14}{3} } \\ \\ = \mathbf{ \binom{4}{4} + \binom{5}{4} + \binom{6}{4} + \binom{7}{4} + \binom{8}{4} + \binom{9}{4} + \binom{10}{4} + \binom{11}{4} + \binom{12}{4} + \binom{13}{4} + \binom{14}{4} + \binom{15}{4} }\\\\ = \mathbf{ \binom{16}{5} }\\\\ = \mathbf{ \dfrac{16!}{5!\cdot 11!} }\\\\ = \mathbf{ \dfrac{12\cdot 13\cdot 14\cdot 15\cdot 16}{5!} }\\\\ = \mathbf{ \dfrac{12\cdot 13\cdot 14\cdot 15\cdot 16}{1\cdot 2\cdot 3\cdot 4\cdot 5} }\\\\ = \mathbf{ \left(\dfrac{12}{3}\right)\cdot 13 \cdot \left(\dfrac{14}{2}\right)\cdot \left(\dfrac{15}{5}\right)\cdot \left(\dfrac{16}{4}\right) }\\\\ = \mathbf{4 \cdot 13 \cdot 7 \cdot 3 \cdot 4}\\\\ = \mathbf{13 \cdot 16 \cdot 21}\\\\ = \mathbf{4368} \end{array} $}}$$

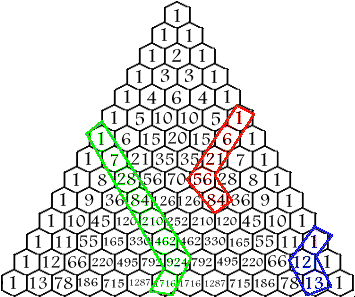$$\[\binom50+\binom51+\binom62+\binom71+\binom83+\binom92+\binom{10}4+\binom{11}3\] = 495$$

somebody pleaes simplify quick 891163 over 9984670

Two numbers 891163 and 9984670 are  relatively prime, because their greatest common divisor equals 1.

You can't simplify the fraction

$$\dfrac{ 891163 }{ 9984670 } = \dfrac{7^2\cdot 13 \cdot 1399} {2\cdot 5 \cdot 53 \cdot 18839}$$

You can also use the function "binom(6,3)"

and the output is

$${\left({\frac{{\mathtt{6}}{!}}{{\mathtt{3}}{!}{\mathtt{\,\times\,}}({\mathtt{6}}{\mathtt{\,-\,}}{\mathtt{3}}){!}}}\right)} = {\mathtt{20}}$$

Wie viel mal 16 ist 192

12 mal 16 ist 192

What is the circumference of a circle with a radius 7.1 cm, to the nearest tenth ?

circumference = $$\pi \cdot d \qquad d = 2\cdot 7.1 ~ \rm{cm} = 14.2 ~ \rm{cm}$$

circumference = $$\pi \cdot 14.2 ~ \rm{cm} \approx 44.1 ~ \rm{cm}$$

factorial definition:

$$\boxed{ n! = n \cdot (n-1)! }$$

Example:  

$$\\5! = 5 \cdot 4! \\ 4! = 4 \cdot 3! \\ 3! = 3 \cdot 2! \\ 2! = 2 \cdot 1! \\ 1! = 1 \cdot 0! \\ 0! = 1 ~ \text{(convention)}\\ \boxed{\,5! = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 \cdot \textcolor[rgb]{150,0,0}{ 1 } \,}$$

Jedes 2 dimensionale Polygon, also auch ein Dreieck, sogar das Zweieck ergibt bei einer Umrundung einen Winkel von $$360 ~ \ensurement{^{\circ}}$$

 Im Dreieck:

                       .

                     .

                   *  $$\alpha_2$$

                 /    \

               /        \

             /            \

           /                \

     $$\alpha_1$$ /                    \

. . . .*------------------*

                     $$\alpha_3$$      \

                                   \

Polygon mit 3 Punkten (Dreieck)   $$\small{\text{$ \alpha_1 + \alpha_2+\alpha_3 = 360 \ensurement{^{\circ}} $}}$$

Allgemein gilt: Polygon mit n Punkten $$\small{\text{$ \alpha_1 + \alpha_2+\alpha_3+ \cdots \alpha_n = 360 \ensurement{^{\circ}} $}}$$