Variables a, b, and c, are positive real numbers.
Prove that:
sqrt(a^2-ab+b^2) + sqrt(a^2-ac+c^2) is greater than or equal to sqrt(b^2+bc+c^2)
Source see: https://math.stackexchange.com/questions/1820957/show-sqrta2-abb2-sqrtb2-bcc2-geq-sqrta2acc2
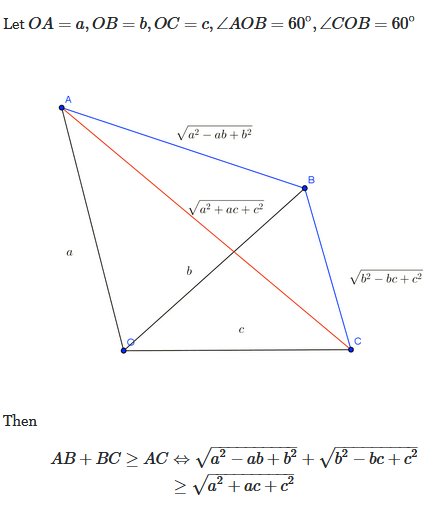
Applying the Law of Cosines:
\(\begin{array}{|rcll|} \hline \mathbf{AB^2} &=& \mathbf{a^2+b^2-2ab\cos(60^\circ)} \quad | \quad \cos(60^\circ) = \dfrac{1}{2} \\ AB^2 &=& a^2+b^2-2ab*\dfrac{1}{2} \\ \mathbf{AB} &=& \mathbf{ \sqrt{a^2-ab+b^2} } \\\\ \mathbf{BC^2} &=& \mathbf{b^2+c^2-2bc\cos(60^\circ)} \quad | \quad \cos(60^\circ) = \dfrac{1}{2} \\ BC^2 &=& b^2+c^2-2bc*\dfrac{1}{2} \\ \mathbf{BC} &=& \mathbf{ \sqrt{b^2-bc+c^2} } \\\\ \mathbf{AC^2} &=& \mathbf{a^2+c^2-2ac\cos(120^\circ)} \quad | \quad \cos(120^\circ) = -\dfrac{1}{2} \\ AC^2 &=& a^2+c^2-2ac*\left(-\dfrac{1}{2}\right) \\ \mathbf{AC} &=& \mathbf{ \sqrt{a^2+ac+c^2} } \\ \hline \end{array} \)
Using the Triangle Inequality, we can get
\(\begin{array}{|rcll|} \hline AB+BC &\ge& AC \\ \mathbf{\sqrt{a^2-ab+b^2} +\sqrt{b^2-bc+c^2}} &\ge& \mathbf{\sqrt{a^2+ac+c^2}} \\ \hline \end{array}\)
Under what conditions does equality occur? That is,
for what values are both sides of the inequality equal?
\(\begin{array}{|lccl|} \hline \text{Let}& \mathbf{\vec{O}} &=& \mathbf{(0,~0)} \\\\ \text{Let}& \vec{A} &=& \Big(a\cos(120^\circ),~a\sin(120^\circ)\Big) \\ & \mathbf{\vec{A}} &=& \mathbf{\Big(-\dfrac{a}{2},~\dfrac{\sqrt{3}}{2}a\Big)} \\\\ \text{Let}& \vec{B} &=& \Big(b\cos(60^\circ),~b\sin(60^\circ)\Big) \\ & \mathbf{\vec{B}} &=& \mathbf{\Big(\dfrac{b}{2},~\dfrac{\sqrt{3}}{2}b\Big)} \\\\ \text{Let}& \mathbf{\vec{C}} &=& \mathbf{(c,~0)} \\ \hline \end{array}\)
Points A, B, and C are on the same line:
\(\begin{array}{|rcll|} \hline \mathbf{ (\vec{c}-\vec{a})\times (\vec{b}-\vec{a} ) } &=& \mathbf{0} \\\\ \left( \left(\begin{array}{c} c \\ 0 \end{array}\right)- \left(\begin{array}{c} -\dfrac{a}{2} \\ \dfrac{\sqrt{3}}{2}a \end{array}\right) \right) \times \left( \left(\begin{array}{c} \dfrac{b}{2} \\ \dfrac{\sqrt{3}}{2}b \end{array}\right)- \left(\begin{array}{c} -\dfrac{a}{2} \\ \dfrac{\sqrt{3}}{2}a \end{array}\right) \right) &=& 0 \\\\ \left(\begin{array}{c} c+\dfrac{a}{2}\\ -\dfrac{\sqrt{3}}{2}a \end{array}\right) \times \left(\begin{array}{c} \dfrac{1}{2}(b+a) \\ \dfrac{\sqrt{3}}{2}(b-a) \end{array}\right) &=& 0 \\\\ \left(c+\dfrac{a}{2}\right) \left(\dfrac{\sqrt{3}}{2}(b-a)\right)- \left( -\dfrac{\sqrt{3}}{2}*\dfrac{a}{2}(b+a) \right) &=& 0 \\\\ \dfrac{\sqrt{3}}{2}\left(c+\dfrac{a}{2}\right)(b-a)+ \dfrac{\sqrt{3}}{2} *\dfrac{a}{2}(b+a) &=& 0 \quad | \quad *\dfrac{2}{\sqrt{3}} \\ \left(c+\dfrac{a}{2}\right)(b-a)+\dfrac{a}{2}(b+a) &=& 0 \\ \left(c+\dfrac{a}{2}\right)(b-a) &=& -\dfrac{a}{2}(b+a) \\ cb-ac+\dfrac{ab}{2}-\dfrac{a^2}{2}&=&-\dfrac{ab}{2}-\dfrac{a^2}{2} \\ cb-ac+\dfrac{ab}{2} &=&-\dfrac{ab}{2} \\ cb-ac+ab &=& 0 \\ cb+ab &=& ac \\ b(a+c) &=& ac \\ \mathbf{b} &=& \mathbf{\dfrac{ac}{a+c}} \\ \hline \end{array}\)
equality occur does under condition: \( \mathbf{b=\dfrac{ac}{a+c}}\)
![]()