heureka

Evaluate 

\(\dfrac{1}{\sqrt5}\cdot\left(\left(\dfrac{1+\sqrt5}{2}\right)^5-\left(\dfrac{1-\sqrt5}{2}\right)^5\right)\)

And DO NOT use a calculator.

The nth element in the Fibonacci series as an analytic function of n is:

\({\displaystyle F_{n}={\cfrac {1}{\sqrt {5}}}\left({\cfrac {1+{\sqrt {5}}}{2}}\right)^{n}-{\cfrac {1}{\sqrt {5}}}\left({\cfrac {1-{\sqrt {5}}}{2}}\right)^{n}~} \)

For n=5 we calculate F₅

\(\begin{array}{|rcll|} \hline F_0 &=& 0 \\ F_1 &=& 1 \\ F_2 &=& F_0 +F_1 = 0+1= 1 \\ F_3 &=& F_1 +F_2 = 1+1= 2 \\ F_4 &=& F_2 +F_3 = 1+2= 3 \\ \mathbf{F_5} &=& F_3 +F_4 = 2+3 \mathbf{= 5} \\ \hline \end{array} \)

Calling all, this is a very nice forum.

3^x=5x

We can use the Lambert W Function.

The link to the Lambert W Function Calculator is:

Hello Melody,

...Euler's formula is true for every polyhedron.

The only polyhedra for which it doesn't work are those that have holes running through them like the one shown in the figure below...

...It involves the Platonic Solids, a well-known class of polyhedra named after the ancient Greek philosopher Plato, in whose writings they first appeared....

What is e=nf/2?

The Platonic Solids:

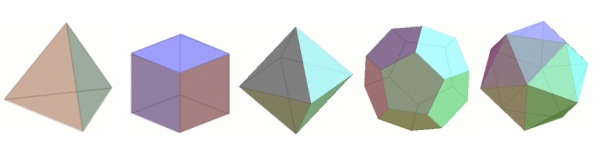
Euler's formula:

V - E + F = 2.

the number of vertices(V), minus the number of edges(E), plus the number of faces(F), is equal to two.

see e=nf/2 in : Proof of five Platonic solids in link:

We have two  different straight lines: {nl} (k-2)x - (k-1)y -7 = 0 and

2x - 7y + 5 = 0 {nl} Find the value of K if those two straight lines are PERPENDICULAR.

Slope line 1 = m₁:

\(\begin{array}{|rcll|} \hline (k-2)x - (k-1)y -7 &=& 0 \quad & | \quad + 7 \\ (k-2)x - (k-1)y &=& 7 \quad & | \quad \cdot (-1) \\ -(k-2)x + (k-1)y &=& -7 \quad & | \quad + (k-2)x \\ (k-1)y &=& -7 + (k-2)x \quad & | \quad :(k-1) \\ y &=& \frac{-7}{k-1} + \underbrace{(\frac{k-2}{k-1} )}_{=m_1}\cdot x \\ \hline \end{array} \)

Slope line 2 = m₂:

\(\begin{array}{|rcll|} \hline 2x - 7y + 5 &=& 0 \quad & | \quad -5 \\ 2x - 7y &=& -5 \quad & | \quad \cdot (-1) \\ -2x + 7y &=& 5 \quad & | \quad + 2x \\ 7y &=& 5 + 2x \quad & | \quad :7 \\ y &=& \frac57 + \underbrace{\frac27}_{=m_2}\cdot x \\ \hline \end{array}\)

PERPENDICULAR: \(m_2 = -\dfrac{1}{m_1}\)

\(\begin{array}{|rcll|} \hline m_2 &=& -\frac{1}{m_1} \quad & | \quad m_1=\frac{k-2}{k-1} \quad m_2=\frac27 \\ \frac27 &=& -\frac{1}{\frac{k-2}{k-1}} \\ \frac27 &=& -\frac{k-1}{ k-2 } \\ 2\cdot (k-2) &=& -7\cdot (k-1) \\ 2k-4 &=& -7k+7 \quad & | \quad + 7k \\ 9k-4 &=& +7 \quad & | \quad + 4 \\ 9k &=& 11 \quad & | \quad : 9 \\ \mathbf{ k } & \mathbf{=} & \mathbf{ \frac{11}{9} } \\ \hline \end{array}\)

Write cos(2 tan⁻¹(x)) as an algebraic expression in x.

\(\begin{array}{|rcll|} \hline && \cos(~2\cdot \underbrace{ tan^{-1}(x) }_{=\varphi}~) \qquad & | \qquad tan^{-1}(x) = \varphi \text{ or } x = \tan(\varphi) \\\\ \text{Formula:} \\ \cos(~2\cdot \varphi) &=& \dfrac{1-\tan^2(\varphi)}{1+\tan^2(\varphi)} \qquad & | \qquad \tan(\varphi) = x\\ \cos(~2\cdot \varphi) &=& \dfrac{1-x^2 }{1+x^2} \\ \mathbf{ \cos(~2\cdot \tan^{-1}(x) ) }& \mathbf{=} & \mathbf{\dfrac{1-x^2 }{1+x^2}} \\ \hline \end{array} \)

the circumference of Terry's wheel is 250 centimeters. Estimate, to 1 significant figure, how many times the wheel goes round when Terry cylces 10 kilometers

\(\begin{array}{|rcll|} \hline && \frac{10\ 000\ m}{2.50\ m} \\\\ &=& 4000 \\\\ &=& 4\cdot 10^3 \\\\ \hline \end{array} \)

The wheel goes round 4000 times.

composition of f(x)=2x^2 and g(x) = x+3 (fog)(x)=?

\(\begin{array}{|rcll|} \hline f(x)=2x^2 \\ g(x)= x+3 \\ && (f\circ g)(x) \\ &=&f\left(\small{g(x)}\right) \\ &=&f\left(\small{x+3}\right) \\ &=& 2\cdot (x+3)^2 \\ &=& 2\cdot (x^2+6x+9) \\ &=& 2x^2+12x+18 \\ \hline \end{array} \)

Es geht um eine Statistik:

Die Bevölkerung lag 1950 bei 83 Millionen, 

nun steigt alle fünf Jahre die Bevölkerung um 6 Prozent,

also das letzte mal 2015.

Nun soll man von dieser letztendlichen Zahl für 2015 35 Prozent nehmen.

Wie viel ist das?

\(\small{ \begin{array}{|lrlcr|l|} \hline \text{Stei-} & \text{Jahr} & & && \text{Bevölkerung}\\ \text{gung} & & & && \text{in Millionen}\\ \hline & 1950 & & && 83\\ 1.& 1955 & 83 + 83\cdot 6\% = 83\cdot (1+0,06)&=& 83\cdot 1,06^1 & 87,98 \\ 2.& 1960 & 83\cdot 1,06 + 83\cdot 1,06 \cdot 6\% = 83\cdot 1,06 \cdot (1+0,06)= 83\cdot 1,06 \cdot 1,06 &=& 83\cdot 1,06^2 & 93,2588 \\ 3.& 1965 & 83\cdot 1,06^2 + 83\cdot 1,06^2 \cdot 6\% = 83\cdot 1,06^2 \cdot (1+0,06)= 83\cdot 1,06^2 \cdot 1,06 &=& 83\cdot 1,06^3 & 98,854\ldots \\ 4.& 1970 & &=& 83\cdot 1,06^{4} & 104,785\ldots \\ 5.& 1975 & &=& 83\cdot 1,06^{5} & 111,072\ldots \\ 6.& 1980 & &=& 83\cdot 1,06^{6} & 117,737\ldots\\ \dots & \dots & \dots &= & \dots & \dots \\ 13.& 2015 & &=& 83\cdot 1,06^{13} & 177,033\ldots \\ \hline \end{array} } \)

\(35 \% \text{ von } 177,033045592\ \text{ Millionen} = \frac{177,033045592\cdot 35 }{100} = 61,9615659572 \ \text{ Millionen}\)