How much is a year ?
Year Definitions
The most common definition in the western world of the year is based on the revolution of the Earth around the Sun and is therefore called a `Solar Year'. However, there are several possibilites to define beginning and end of one revolution and thus also several kinds of solar years:
The years so defined differ in length because of the precession of Earth's rotation and the tumbling of the Earth orbit.
Julian year (365.25 days UT) and Gregorian year (365.2425 days UT) as defined in the calendars of the respective name are solar years as well.
See: http://www.maa.mhn.de/Scholar/calendar.html#def
![]()
Hallo Omi67,
Deine 2. Lösung sin(x2) = -0.85746025108 mit dem Winkel x2 = -59.0326049162
erfüllt nicht die Ausgangsgleichung:
0,9*cos(x)-0,75*sin(x)=0,18
0,9*cos(-59,0326049162) - 0,75 * sin(-59,0326049162)
= 0,9* 0,51455020923 -0.75*(-0.85746025108)
= 0.46309518831 + 0.64309518831 = 1.10619037662 $$\ne$$ 0.18
Siehe Link zur Lösung mit WolframAlpha:
http://www.wolframalpha.com/input/?i=0.9*+cos%28x%29-0.75*sin%28x%29%3D0.18
Viele Grüße
Heureka
Die horizontale Sichtweite ( horizon distance ) aus 400 km Höhe ( ISS ) auf die Erde soll nach einer Berechnung 2294 km betragen
Wie kann man das berechnen ?
Mit Hilfe des Tangentensatzes!
Gegeben sei ein Kreis k mit einer Sekante g und einer Tangente t, die sich in einem Punkt S außerhalb des Kreises schneiden. Bezeichnet man die Schnittpunkte des Kreises k mit g als  beziehungsweise
beziehungsweise 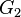 und den Berührpunkt der Tangente als
und den Berührpunkt der Tangente als  , so gilt:
, so gilt:

https://de.wikipedia.org/w/index.php?title=Datei:SekTangSatz.png&filetimestamp=20040728160144&
$$\small{\text{$\boxed{t^2=h(h+2\cdot R)}$}}\\\\
\small{\text{
$t^2=400\cdot ( 400 + 2\cdot 6378,137 )
$}}\\
\small{\text{
$t^2=400\cdot ( 400 + 12756,274)
$}}\\
\small{\text{
$t^2=400\cdot ( 13156,274)
$}}\\
\small{\text{$ t^2=5262509,6$}}\\
\small{\text{$ t=\sqrt{5262509,6}$}}\\
\small{\text{$ t=2294,016\ \rm{km}$}}$$
https://de.wikipedia.org/wiki/Sekanten-Tangenten-Satz
![]()