hectictar

3.

midpoint of  (6, 12)  and  (0, -6)  =  $\Big( \frac{6+0}{2},\frac{12+-6}{2}\Big)\ =\ \Big(\frac62,\frac62\Big)\ =\ (3,3)$

sum of coordinates of  (3, 3)  =  3 + 3  =  6

1.

distance between  (1, 1)  and  (4, 7)  =  $\sqrt{(4-1)^2+(7-1)^2}\ =\ \sqrt{9+36}\ =\ \sqrt{45}\ =\ 3\sqrt5$

2.

The ratio of their side lengths is...

$\sqrt{\frac{192}{80}}\ =\ \sqrt{\frac{12}{5}}\ =\ \frac{\sqrt{12}}{\sqrt5}\ =\ \frac{\sqrt{12}\,\cdot\,\sqrt5}{\sqrt5\,\cdot\,\sqrt5}\ =\ \frac{\sqrt{12\,\cdot\,5}}{\sqrt{5\,\cdot\,5}}\ =\ \frac{\sqrt{2\,\cdot\,2\,\cdot\,3\,\cdot\,5}}{\sqrt{5\,\cdot\,5}}\ =\ \frac{\sqrt{2\,\cdot\,2}\,\cdot\,\sqrt{3\,\cdot\,5}}{\sqrt{5\,\cdot\,5}}\ =\ \frac{2\sqrt{15}}{5}$

Now it is in the simplified form  $\frac{a\sqrt{b}}{c}$  where  a,  b,  and  c  are integers.

a + b + c  =  2 + 15 + 5  =  22

b)

You can try looking at that graph and moving the point until the y-value goes just above 15 .

But to find the answer without using that....

Let's find values of  t  which make  h(t)  =  15

$15\ =\ -8\cos(\frac{\pi t}{10})+9\\~\\ 6\ =\ -8\cos(\frac{\pi t}{10})\\~\\ -\frac34\ =\ \cos(\frac{\pi t}{10})$

There are two values of  $\frac{\pi t}{10}$  in the interval  [0, 2π)  and thus two values of  t  which make  $\cos(\frac{\pi t}{10})=-\frac34$

They are:

$\begin{array}{} \frac{\pi t}{10}\ =\ \arccos(-\frac34)&\quad&\frac{\pi t}{10}\ =\ 2\pi-\arccos(-\frac34)\\~\\ t\ =\ \frac{10}{\pi}\arccos(-\frac34)&&t\ =\ \frac{10}{\pi}(2\pi-\arccos(-\frac34))\\~\\ t\ \approx\ 7.7&&t\ =\ 20-\frac{10}{\pi}\arccos(-\frac34)\\~\\ &&t\ \approx\ 20-7.7\\~\\ &&t\ \approx\ 12.3 \end{array}$

The height is 15 meters 7.7 seconds after the starting position and again 7.7 seconds before the starting position.

So we can see that Bobby will be really nervous when  t  is in the interval  (7.7, 12.3)

Bobby will be really nervous again 20 seconds later when the Ferris wheel is back at the same spot, so

Bobby will be really nervous when  t  is in the interval  (27.7,  32.3)

a)

Maybe this drawing will help...

The thing at the bottom right corner of the triangle is supposed to be somebody riding the Ferris wheel x)

All the lengths are in meters, and  t  is the number of seconds after the ride starts.

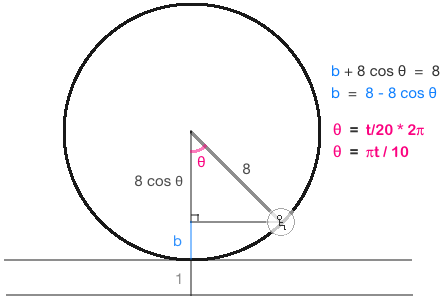
height of person  =  b + 1

height of person  =  8 - 8 cos θ  + 1

height of person  =  9 - 8 cos θ

height of person  =  9 - 8 cos( $\frac{\pi t}{10}$ )

h(t)  =  -8 cos( $\frac{\pi t}{10}$ ) + 9

If you have a question about where any part of this came from, please ask

$d\ =\ \sqrt{(1-5)^2+(\sqrt2-\sqrt8)^2}$          But   $\sqrt2-\sqrt8\ \neq\ -2$    !!

$d\ =\ \sqrt{(1-5)^2+(\sqrt2-2\sqrt2)^2}$          because   $\sqrt8\ =\ 2\sqrt{2}$

$d\ =\ \sqrt{(1-5)^2+(-\sqrt2\,)^2}$          because   x - 2x  =  -x    so     $\sqrt2-2\sqrt2\ =\ -\sqrt2$

$d\ =\ \sqrt{(-4)^2+(-\sqrt2\,)^2}$          because  1 - 5  =  -4

$d\ =\ \sqrt{16+2}$          because   $(-4)^2=16$     and     $(-\sqrt2)^2=2$

$d\ =\ \sqrt{18}$

$d\ =\ 3 \sqrt{2}$_

$(2,3)$  is at the polar coordinates of  $(r,\theta)$  so:

$2\ =\ r\cos\theta\\~\\ 3\ =\ r\sin\theta$

$(x_1,y_1)$  is at the polar coordinates of  $(2r,\theta+\frac{\pi}{2})$  so:

$\begin{array}{} x_1\ =\ (2r)\cos(\theta+\frac{\pi}{2})&=&(2r)(-\sin\theta)&=&(-2)(r\sin\theta)&=&(-2)(3)&=&-6\\~\\ y_1\ =\ (2r)\sin(\theta+\frac{\pi}{2})&=&(2r)(\cos\theta)&=&(2)(r\cos\theta)&=&(2)(2)&=&4 \end{array}$

$(x_2,y_2)$  is at the polar coordinates of  $(-r,-\theta)$  so:

$\begin{array}{c} x_2\ =\ (-r)\cos(-\theta)&=&(-r)\cos\theta&=&-(r\cos\theta)&=&-2\\~\\ y_2\ =\ (-r)\sin(-\theta)&=&(-r)(-\sin\theta)&=&r\sin\theta&=&3 \end{array}$_

1 + 2 + 3 - 4 + 5 + 6

We want to subtract as much as possible. So the minimum possible value this expression can obtain is

1 + 2 + 3 - (4 + 5 + 6)   =   6 - 15   =   -9

n₁  =  0

n₂  =  1

n₃  =  6

n₄  =  2

n_k  =  n_{(k mod 4)}     and     n₀  =  n₄

$\ \phantom{=\quad}\frac43x^2+4x+1$

                                                   Factor  $\frac43$  out of all the terms.

$=\quad\frac43(x^2+3x+\frac34)$

                                                          Add  $\frac94$  and subtract  $\frac94$  to complete the square inside the parenthesees.

$=\quad\frac43(x^2+3x+\frac{9}{4}-\frac{9}{4}+\frac34)$

                                                          Factor   $x^2+3x+\frac94$   as a perfect square trinomial.

$=\quad\frac43(\ (x+\frac32)^2-\frac{9}{4}+\frac34)$

                                                          Combine  $-\frac94$  and  $+\frac34$

$=\quad\frac43(\ (x+\frac32)^2-\frac{6}{4})$

                                                   Distribute the  $\frac43$

$=\quad\frac43(x+\frac32)^2-\frac43(\frac{6}{4})$

                                                   And  $\frac43(\frac64)\ =\ 2$

$=\quad\frac43(x+\frac32)^2-2$

Now the expression is in the form  a(x + b)² + c  where  a,  b,  and  c  are constants.

$abc\ =\ (\frac43)(\frac32)(-2)\ =\ (2)(-2)\ =\ -4$ _