Let's say it starts wih x fish.
| number of fish left after | John | leaves | _ | \(=\ \frac23({\color{Aquamarine}x}-1)\ =\ \frac23x-\frac23\) |
| number of fish left after | Joe | leaves |
| \(=\ \frac23(\ {\color{Aquamarine}\frac23x-\frac23}\ -1)\ =\ \frac49x-\frac{10}{9}\) |
| number of fish left after | _James_ | leaves |
| \(=\ \frac23(\ {\color{Aquamarine}\frac49x-\frac{10}{9}}\ -1)\ =\ \frac{8}{27}x-\frac{38}{27}\) |
The smallest positive integer value of x that makes \(\frac{8}{27}x-\frac{38}{27}\) a positive integer is 25 .
By looking at a graph we can check this: https://www.desmos.com/calculator/mivvh3t6in
So the minimum possible number of fish before John threw out the first fish is 25 .
The endpoints of s2 are 3 to the right and 2 down from the endpoints of s1
s1 has endpoints at (1, 2) and (7, 10)
s2 has endpoints at (1 + 3, 2 - 2) and (7 + 3, 10 - 2)
s2 has endpoints at (4, 0) and (10, 8)
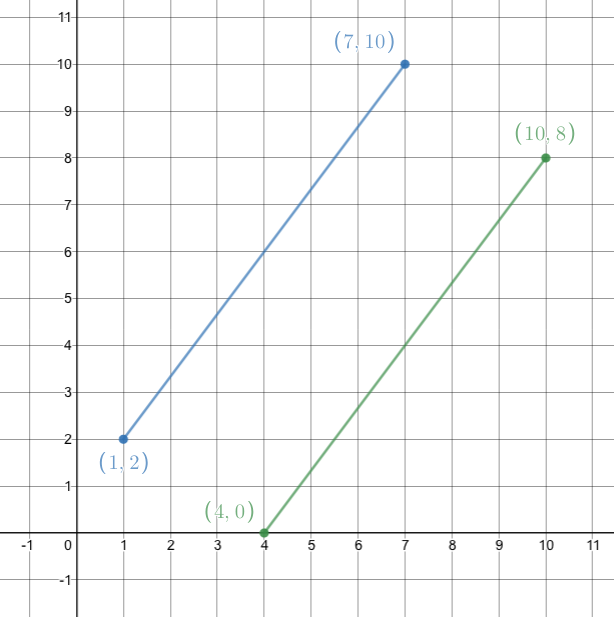
https://www.desmos.com/calculator/g6yqktgtvp
midpoint of s2 = \(\Big( \frac{4+10}{2},\frac{0+8}{2} \Big)\ =\ \Big(\frac{14}{2},\frac82\Big)\) = (7, 4)
point M = midpoint of segment PR = \(\Big( \frac{1+7}{2},\frac{3+15}{2}\Big)\ =\ \Big( \frac{8}{2},\frac{18}{2}\Big)\) = (4, 9)
To reflect segment PR over the x-axis, we make the y-coordinate of each of its points negative. So...
image of point M = (4, -9)
sum of the coordinates of the image of point M = 4 + -9 = -5
Here's a graph: https://www.desmos.com/calculator/bmiffafl6d