This is an especially tricky question because they do not give us an exact triangle ABC.
Here is a graph to see different possible scenarios: https://www.desmos.com/calculator/t4tcx4ev8m
We can change the length of reachable fence by moving the points so that part of AC is inside the circle without violating any of the rules given in the problem statement. So I would venture to say this is a bad question. I will just make the significant assumption that no part of AC is inside the circle.
Here is a diagram with new points D, E, and F labeled as shown:
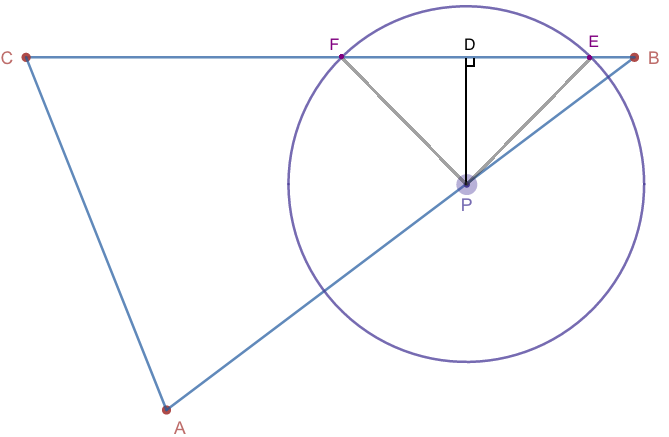
length of reachable fence = diameter of circle P + length of chord EF
Let all lengths be in meters.
diameter of circle P = 2 * radius of circle P = 2 * 3.8 = 7.6
| Let's look at △BDP . | ____ | |||
| sin 37° = DP / BP | because △BDP is a right triangle and m∠DBP = 37° |
| ||
| sin 37° = DP / 4.5 | because BP = 4.5 | |||
| 4.5 sin 37° = DP |
|
| ||
| Now let's look at △DEP . |
|
| ||
| ( DE )2 + ( DP )2 = ( EP )2 |
| by the Pythagorean Theorem. |
| |
| ( DE )2 + ( 4.5 sin 37°)2 = ( 3.8 )2 |
| because DP = 4.5 sin 37° and EP = radius of circle P = 3.8 |
| |
| ( DE )2 = ( 3.8 )2 - ( 4.5 sin 37°)2 |
| |||
| DE = √[ ( 3.8 )2 - ( 4.5 sin 37°)2 ] |
|
| ||
| DE ≈ 2.67 | ||||
And by the hypotenuse-leg congruence theorem, △DEP ≅ △DFP . So DE = DF
length of chord EF = DE + DF = DE + DE = 2 * DE ≈ 2 * 2.67 ≈ 5.34
length of reachable fence = diameter of circle P + length of chord EF ≈ 7.6 + 5.34 ≈ 12.9
a.
If you take the graph of f and multiply the y-coordinates of every point by \(\frac12\) , that will vertically compress the graph
If you take the graph of f and multiply the y-coordinates of every point by -1 , that will reflect the graph over the x-axis.
So the graph of function g is the graph of function f vertically compressed and reflected over the x-axis.
I'm not entirely sure what the function notation is, but I think it is this:
g(x) = -\(\frac12\) f(x)
(Also........I wanted to say "vertically compressed by a factor of 2" or "vertically compressed by a factor of \(\frac12\) " but I didn't know which is considered correct, and the only thing I could find about this question was here: http://mathforum.org/library/drmath/view/77603.html. It seems like there's not a universally accepted way of stating it, so I just left it out!)
b.
f(x) = -x2 + 2
h(x) = 7x2 + b
We can see the factor must be -7 .
h(x) = -7 f(x) = -7( -x2 + 2 ) = 7x2 - 14
h(x) = 7x2 - 14 so we can see that b = -14
1.
\(\dfrac{\frac{1}{x^2}+\frac{2}{y}}{\frac5x-\frac{6}{y^2}}\ =\ \dfrac{\frac{1}{x^2}+\frac{2}{y}}{\frac5x-\frac{6}{y^2}}{\color{blue}\ \cdot\dfrac{x^2y^2}{x^2y^2}}\ =\ \dfrac{y^2+2x^2y}{5xy^2-6x^2}\) and y ≠ 0
2.
To graph \(y\geq-\frac12x+2\frac12\) , graph the line \(y=-\frac12x+2\frac12\) then lightly shade the portion above the line.
To graph \(y<\frac15x+6\) , graph the line \(y=\frac15x+6\) but make it a dotted line. Then lightly shade the portion below it.
The solution to the system of inequalities is the portion of the graph that is shaded twice.
See here: https://www.desmos.com/calculator/hzox2qggig
According to the graph, the point (0, 4) should satisfy both inequalities.
Is it true that \(4\geq-\frac12(0)+2\frac12\) ? Yes it is true that \(4\geq2\frac12\)
Is it true that \(4<\frac15(0)+6\) ? Yes it is true that \(4<6\)
So (0, 4) does satisfy both inequalities.