heureka

 If $n \equiv 2 \pmod{7}$,
 then find the remainder when
 $(n + 2)(n + 4)(n + 6)$ is divided by $7$.

$\begin{array}{|rcll|} \hline \mathbf{(n + 2)(n + 4)(n + 6) \pmod{7}} &\equiv& (2 + 2)(2 + 4)(2 + 6) \pmod{7} \\ &\equiv& 4*6*8 \pmod{7} \\ &\equiv& 192 \pmod{7} \\ &\equiv& {\color{red}3} \pmod{7} \\ \hline \end{array}$

If I expand
$25*24*23* \dotsm *12*11*10$,
how many zeros are there at the end of the number I get?

$25*24*23* \dotsm *12*11*10 = 25!-9!$

$\begin{array}{|rcll|} \hline \text{zeros} &=& \lfloor\frac{25}{5}\rfloor +\lfloor\frac{25}{25}\rfloor -\lfloor\frac{9}{5}\rfloor \\ &=& 5+1-1 \\ \mathbf{\text{zeros}} &=& \mathbf{5} \\ \hline \end{array}$

If
$z = \dfrac{ \left\{ \sqrt{3} \right\}^2 - 2 \left\{ \sqrt{2} \right\}^2 }{ \left\{ \sqrt{3} \right\} - 2 \left\{ \sqrt{2} \right\} }$
find $\lfloor z \rfloor$.

$\begin{array}{|rcll|} \hline z &=& \dfrac{ \left\{ \sqrt{3} \right\}^2 - 2 \left\{ \sqrt{2} \right\}^2 }{ \left\{ \sqrt{3} \right\} - 2 \left\{ \sqrt{2} \right\} } \\\\ z &=& \dfrac{ (\sqrt{3}-1)^2 - 2 (\sqrt{2}-1)^2 } { \sqrt{3}-1 - 2 (\sqrt{2}-1) } \\\\ z &=& \dfrac{ 3-2\sqrt{3}+1 -2(2-2\sqrt{2}+1) } { \sqrt{3}-2\sqrt{2}+1 } \\\\ z &=& \dfrac{ -2\sqrt{3}+4\sqrt{2}-2 } { \sqrt{3}-2\sqrt{2}+1 } \\\\ z &=& \dfrac{ -2(\sqrt{3}-2\sqrt{2}+1) } { \sqrt{3}-2\sqrt{2}+1 } \\\\ z &=& -2 \\\\ \lfloor z \rfloor &=& -2 \\ \hline \end{array}$

Let $P = 4^{1/4} \cdot 16^{1/16} \cdot 64^{1/64} \cdot 256^{1/256} \dotsm$
Then $P$ can be expressed in the form $\sqrt[a]{b}$,
where $a$ and $b$ are positive integers.
Find the smallest possible value of $a+b$

$\begin{array}{|rcll|} \hline P &=& 4^{1/4} \cdot 16^{1/16} \cdot 64^{1/64} \cdot 256^{1/256} \dotsm \\ P &=& 2^{\frac{1}{2^1}} \cdot 2^{\frac{2}{2^3}} \cdot 2^{\frac{3}{2^5}} \cdot 2^{\frac{4}{2^7}} \dotsm 2^{\left(\frac{n}{2^{2n-1}} \right)} \dotsm \\ P &=& 2^{\frac{1}{2^1}+\frac{2}{2^3}+\frac{3}{2^5}+\frac{4}{2^7}+\dotsm+\frac{n}{2^{2n-1}}+\dotsm } \\ P &=& 2^{S_{\infty}} \\ \hline S_n &=& \frac{1}{2^1}+\frac{2}{2^3}+\frac{3}{2^5}+\frac{4}{2^7}+\dotsm+\frac{n}{2^{2n-1}} \\ \frac{1}{2^2}S_n &=& \frac{1}{2^3}+\frac{2}{2^5}+\frac{3}{2^7}+\dotsm+\frac{n-1}{2^{2n-1}} +\frac{n}{2^{2n+1}}\\ \hline S_n-\frac{1}{2^2}S_n &=& \frac{1}{2^1}+\frac{1}{2^3}+\frac{1}{2^5}+\frac{1}{2^7}+\dotsm+\frac{1}{2^{2n-1}}-\frac{n}{2^{2n+1}} \\ \frac{3}{4}S_n &=& s-\frac{n}{2^{2n+1}}\qquad (1) \\ s&=& \frac{1}{2^1}+\frac{1}{2^3}+\frac{1}{2^5}+\frac{1}{2^7}+\dotsm+\frac{1}{2^{2n-1}} \\ \frac{1}{2^2}s &=& \frac{1}{2^3}+\frac{1}{2^5}+\frac{1}{2^7}+\dotsm+\frac{1}{2^{2n-1}}+\frac{1}{2^{2n+1}} \\ \hline s-\frac{1}{2^2}s &=&\frac{1}{2^1} - \frac{1}{2^{2n+1}} \\ \frac{3}{4}s &=&\frac{1}{2^1} - \frac{1}{2^{2n+1}} \\\\ s &=& \frac{4}{3}* \left( \frac{1}{2^1} - \frac{1}{2^{2n+1}} \right) \\ \hline \frac{3}{4}S_n &=& s-\frac{n}{2^{2n+1}}\qquad (1) \\ \frac{3}{4}S_n &=& \frac{4}{3}* \left( \frac{1}{2^1} - \frac{1}{2^{2n+1}} \right)-\frac{n}{2^{2n+1}} \\ \frac{3}{4}S_{\infty} &=& \frac{4}{3}* \left( \frac{1}{2^1} - 0 \right)-0 \\ \frac{3}{4}S_{\infty} &=& \frac{2}{3} \\ S_{\infty} &=& \frac{4}{3}*\frac{2}{3} \\ S_{\infty} &=& \frac{8}{9} \\ \hline P &=& 2^{S_{\infty}} \\ P &=& 2^{\frac{8}{9}} \\ P &=& \sqrt[9]{2^8} \\ P &=& \sqrt[9]{256} \\ \hline \end{array}$

$\begin{array}{|rcll|} \hline a+b &=& 9+256 \\ \mathbf{a+b} &=& \mathbf{265} \\ \hline \end{array}$

How many zeros are at the end of $(100!)(200!)(300!)(400!)$

when multiplied out?

In the diagram below, EU = 8, UF = 7,GV = 5, VH = 15, and UV= 8.
Find XY.

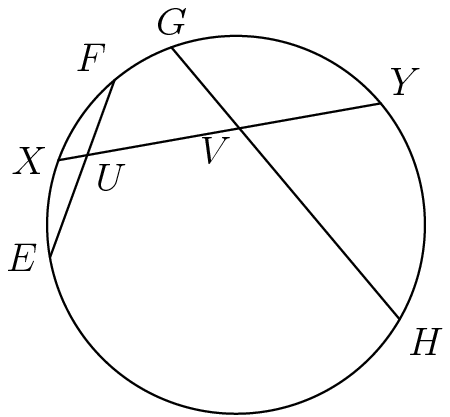
$\begin{array}{|rcll|} \hline EU*UF &=& XU*UY \quad | \quad UY=(UV+VY) \\ EU*UF &=& XU*(UV+VY) \\ 8*7 &=& XU*(8+VY) \\ 56 &=& XU*(8+VY) \qquad (1) \\ 56 &=& 8XU+XU*VY \\ XU*VY &=& 56-8XU \qquad (2) \\ \hline \end{array}$

$\begin{array}{|rcll|} \hline GV*VH &=& XV*VY \quad | \quad XV=(XU+UV) \\ GV*VH &=& VY*(XU+UV) \\ 5*15 &=& VY*(8+XU) \\ 75 &=& VY*(8+XU) \qquad (3) \\ 75 &=& 8VY+XU*VY \\ XU*VY &=& 75-8VY \qquad (4) \\ \hline \end{array}$

$\begin{array}{|lrcll|} \hline (2)=(4) : & 56-8XU &=& 75-8VY \\ & 8VY &=& 19+8XU \\\\ & VY &=& \dfrac{19+8XU}{8} \qquad (5) \\\\ \hline (2)=(4) : & 56-8XU &=& 75-8VY \\ & 8XU &=& -19+8VY \\\\ & XU &=& \dfrac{-19+8VY}{8} \qquad (6) \\ \hline \end{array}$

$\begin{array}{|lrcll|} \hline \text{put}~(6)~\text{into}~(1):& 56 &=& \dfrac{-19+8VY}{8}*(8+VY) \\\\ &8* 56 &=& (-19+8VY)*(8+VY) \\ &448 &=& (-19+8VY)*(8+VY) \\ & 448 &=& -152-19VY+64VY+8VY^2 \\ &8VY^2+45VY-600 &=& 0 \\ \hline &VY &=& \dfrac{-45+\sqrt{21225} }{16} \\ \hline \end{array}$

$\begin{array}{|lrcll|} \hline \text{put}~(5)~\text{into}~(3):& 75 &=& \dfrac{19+8XU}{8}*(8+XU) \\\\ & 8*75 &=& (19+8XU)*(8+XU) \\ & 600 &=& (19+8XU)*(8+XU) \\ & 600 &=& 152 +19XU+64XU+8XU^2 \\ & 8XU^2 + 83XU-448 &=& 0 \\ \hline &XU &=& \dfrac{-83+\sqrt{21225} }{16} \\ \hline \end{array}$

$\begin{array}{|rcll|} \hline XY &=& UV+XU+VY \\\\ XY &=& 8 + \dfrac{-83+\sqrt{21225} }{16} + \dfrac{-45+\sqrt{21225} }{16} \\\\ XY &=& 8 - \dfrac{83}{16} + \dfrac{\sqrt{21225} }{16} - \dfrac{45}{16} + \dfrac{\sqrt{21225} }{16} \\\\ XY &=& 8 - \dfrac{83+45}{16} + \dfrac{2*\sqrt{21225} }{16} \\\\ XY &=& 8 - 8+ \dfrac{2*\sqrt{21225} }{16} \\\\ XY &=& \dfrac{\sqrt{21225} }{8} \\\\ XY &=& \dfrac{5\sqrt{849} }{8} \\\\ XY &\approx& 18.211 \\ \hline \end{array}$

Find the last two digits of the following sum: $5! + 6! + 7! + 8! + 9! + \ldots + 100!$

Five angles of a hexagon measure
$119^\circ,~ 129^\circ,~ 140^\circ,~ 129^\circ,~$ and $95^\circ$.
What is the measure of the sixth angle?

$\begin{array}{|rcll|} \hline \small{119^\circ+129^\circ+140^\circ+129^\circ+95^\circ + x} &=& 4*180^\circ \\ x &=& \small{4*180^\circ -119^\circ+129^\circ+140^\circ+129^\circ+95^\circ} \\ x &=& 108^\circ \\ \hline \end{array}$

Given 4*10^(2-x)=3*e^(2x+3) what would be the value of x?

$\begin{array}{|rcll|} \hline 4*10^{2-x}&=&3*e^{2x+3} \\\\ && \boxed{ 10^{2-x}=e^{(2-x)\ln(10)}} \\\\ 4*e^{(2-x)\ln(10)}&=&3*e^{2x+3} \\\\ \dfrac{4}{3} &=& \dfrac{e^{2x+3}} {e^{(2-x)\ln(10)}} \\\\ \dfrac{4}{3} &=& e^{2x+3-(2-x)\ln(10)} \\\\ \dfrac{4}{3} &=& e^{2x+3-2\ln(10)+x\ln(10)} \\\\ \ln \left(\dfrac{4}{3} \right) &=& \ln\left( e^{2x+3-2\ln(10)+x\ln(10)} \right) \\\\ \ln \left(\dfrac{4}{3} \right) &=& 2x+3-2\ln(10)+x\ln(10) \\\\ 2x+x\ln(10) &=& \ln \left(\dfrac{4}{3} \right)+2\ln(10)-3 \\\\ x\Big(2+\ln(10)\Big) &=& \ln \left(\dfrac{4}{3} \right)+\ln(10^2)-3 \\\\ x\Big(2+\ln(10)\Big) &=& \ln \left(\dfrac{4*10^2}{3} \right)-3 \\\\ x\Big(2+\ln(10)\Big) &=& \ln \left(\dfrac{400}{3} \right)-3 \\\\ \mathbf{x} &=& \mathbf{ \dfrac{\ln \left(\dfrac{400}{3} \right)-3} {2+\ln(10)} } \\ \hline \end{array}$

What is the numerical value of $x$:
$x = \dfrac{1}{3-\dfrac{1}{3-\dfrac{1}{3-\ldots}}}$

$\begin{array}{|rcll|} \hline x &=& \dfrac{1}{3-\dfrac{1}{3-\dfrac{1}{3-\ldots}}} \\\\ x &=& \dfrac{1}{3-x} \\\\ x(3-x) &=& 1 \\\\ 3x-x^2 &=& 1 \\\\ \mathbf{x^2-3x+1} &=& \mathbf{0} \\\\ x &=& \dfrac{3\pm \sqrt{9-4*1} }{2} \\\\ x &=& \dfrac{3\pm \sqrt{5} }{2} \\\\ \mathbf{x} &=& \mathbf{\dfrac{3-\sqrt{5} } {2} } \\ \hline \end{array}$