hectictar

1 and 2)

m∠KJL  =  m∠DJC  because they are vertical angles

m∠JKL  =  m∠JDC  because they are alternate interior angles

So by AA similarity, △JKL is similar to △JDC

The option you have selected is correct

We can also solve for  x  like this:

$\frac12$( 2x - 14 )  =  4

                                Multiply both sides of the equation by  2

2x - 14  =  8

                                Add  14  to both sides.

2x  =  22

                                Divide both sides by  2

x  =  11

This way we avoid disributing the  $\frac12$ . In this particular case it was shorter to do it the way CoolStuffYT said, but in many other cases it is easier to work it the other way. For example:

$\frac12$( x - 14 )  =  4

In this example, it is easier to first multiply both sides by  2  rather than distribute  $\frac12$ .

Try it both ways and you can see why

Let half the width of the rectangle  =  w

Then half the length of the rectangle  =  √[ 1 - w² ]

And let the area of the rectangle  =  A

$A\ =\ 4w\sqrt{1-w^2}\\~\\ \frac{dA}{dw}\ =\ 4\frac{d}{dw}\big(w\sqrt{1-w^2}\,\big)\\~\\ \frac{dA}{dw}\ =\ 4\Big[(w)(\frac12)(1-w^2)^{-\frac12}(-2w)+(\sqrt{1-w^2})(1)\Big]\\~\\ \frac{dA}{dw}\ =\ 4\Big[\frac{-w^2}{\sqrt{1-w^2}}+\sqrt{1-w^2}\Big]\\~\\ \frac{dA}{dw}\ =\ 4\Big[\frac{-w^2}{\sqrt{1-w^2}}+\frac{1-w^2}{\sqrt{1-w^2}}\Big]\\~\\ \frac{dA}{dw}\ =\ \frac{4-8w^2}{\sqrt{1-w^2}}$

Now let's find what value of  w  makes  $\frac{dA}{dw}$  be  0 .

$0\ =\ \frac{4-8w^2}{\sqrt{1-w^2}}\\~\\ 0\ =\ 4-8w^2\qquad\text{and}\qquad\sqrt{1-w^2}\ \neq\ 0\qquad\text{that is}\qquad w\ \neq\ \pm1\\~\\ 8w^2\ =\ 4\\~\\ w^2\ =\ \frac12\\~\\ w\ =\ \sqrt{\frac12}\qquad\text{or}\qquad w\ =\ -\sqrt{\frac12}$

We know half the width of the rectangle can't be negative,

Note that there is a rule which says  sin( 90° - θ )  =  cos( θ )  for any angle measure  θ . So...

sin( 78° )  =  sin( 90° - 12° )  =  cos( 12° )  =  h

(2)  Here is a sketch of a single face of the regular pentagonal pyramid:

Remember there are  5  faces total because a pentagon has  5  sides. So....

lateral area  =  5 * area of triangular face

lateral area  =  5 * (1/2)(18)( s )

We can find  s  with the Pythagorean theorem:

9² + s²  =  16²

s²  =  16² - 9²

s²  =  175

s  =  √[ 175 ]

s  =  5√7

lateral area  =  5 * (1/2)(18)( 5√7 )

lateral area  =  225√7  square units

(1)

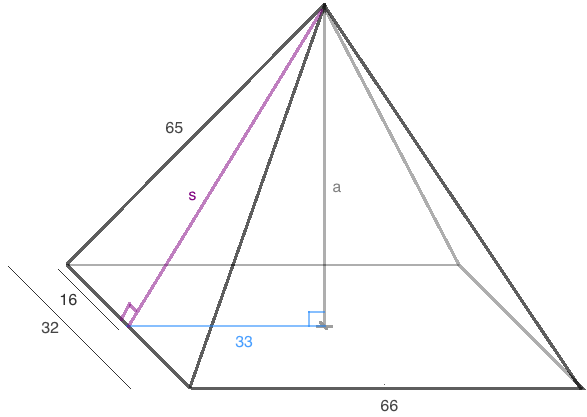
Here,  s  is a slant height and  a  is the altitude.

We can find  s  with the Pythagorean theorem.

s² + 16²  =  65²

s²  =  65² - 16²

s²  =  3969

s  =  63

Now we can find  a  with the Pythagorean theorem.

a² + 33²  =  s²

a² + 33²  =  63²

a²  =  63² - 33²

a²  =  2880

a  =  √[ 2880 ]

a  =  24√5

*****edit*****

My original answer for lateral area wasn't right because I didn't take into account that the faces aren't all the same.

The same way we found  s ,  we can find the length of the other slant height.

other slant height  =  √[ 65² - 33² ]  =  56

lateral area   =   2 * (1/2) * 32 * 63   +   2 * (1/2) * 66 * 56   =   32 * 63  +  66 * 56   =   5712  square units

Again, the standard form of a line is  Ax + By = C  where A is a positive integer, and B and C are integers.

Using the point  (-2, -3)  and the slope  $\frac12$ ,  the equation of the line in point-slope form is:

y - -3  =  $\frac12$(x - -2)

y + 3  =  $\frac12$(x + 2)

                                   Multiply both sides of the equation by  2 .

2(y + 3)  =  1(x + 2)

                                   Distribute.

2y + 6  =  x + 2

                                   Subtract  2y  from both sides.

6  =  x - 2y + 2

                                   Subtract  2  from both sides.

4  =  x - 2y

x - 2y  =  4

We're given a point and a slope so we can easily write the equation of the line in point-slope form.

The equation of the line in point-slope form is....

y - -4  =  -$\frac38$(x - 5)

Now we just need to get this equation into standard form.

The standard form of a line is  Ax + By = C  where A is a positive integer, and B and C are integers.

y - -4  =  -$\frac38$(x - 5)

y + 4  =  -$\frac38$(x - 5)

                                     Multiply both sides of the equation by  8 .

8(y + 4)  =  -3(x - 5)

                                     Distribute the  8  and the  -3

8y + 32  =  -3x + 15

                                     Add  3x  to both sides of the equation.

3x + 8y + 32  =  15

                                     Subtract  32  from both sides.

3x + 8y  =  -17

The line appears to cross the y-axis at the point  (0, -1)  , so the y-intercept is  -1 .

The points  (1, 0)  and  (0, -1)  appear to be on the line. Using these two points we can find the slope.

slope  =  $\frac{\text{rise}}{\text{run}}\ =\ \frac{y_2-y_1}{x_2-x_1}\ =\ \frac{-1-0}{0-1}\ =\ \frac{-1}{-1}\ =\ 1$

Now we know the y-intercept is  -1  and the slope is  1. So the equation of this line in slope-intercept form is....

y  =  1x - 1

y  =  x - 1

Also....

We can see that the slope is  1  by counting the units on the graph. To get from the point  (0, -1)  to the point  (1, 0)

we have to go up 1 unit and to the right 1 unit, so the slope  =  1/1  =  1