hectictar

The only way I could think of to do it was with the Law of Cosines too, but I will definitely try to remember Appollonius's Theorem from now on

Rationalize the denominator of $\frac{5}{2+\sqrt{6}}$. The answer can be written as $\frac{A\sqrt{B}+C}{D}$, where A, B, C, and D are integers, D is positive, and B is not divisible by the square of any prime. If the greatest common divisor of A, C, and D is 1, find A+B+C+D.

__________

$\frac{5}{2+\sqrt{6}}\,=\,\frac{5}{2+\sqrt6}\cdot\frac{2-\sqrt6}{2-\sqrt6}\,=\,\frac{10-5\sqrt6}{4-6}\,=\,\frac{10-5\sqrt6}{-2} \,=\,\frac{5\sqrt6-10}{2}$

Now it is in the form  $\frac{A\sqrt{B}+C}{D}$   and...

A, B, C, and D  are integers

D  is positive

B  is not divisible by the square of any prime

the GCF of  A, C, and D  =  the GCF  of  5, -10, and 2  =  1

A + B + C + D  =  5 + 6 + -10 + 2  =  3

I have never heard of Appollonius's Theorem, but does seem like it can be used here.

Let  $a^2=\frac{16}{44}$  and  $b^2=\frac{(2+\sqrt{5})^2}{11}$ , where  $a$  is a negative real number and  $b$  is a positive real number.

If  $(a+b)^3$  can be expressed in the simplified form  $\frac{x\sqrt{y}}{z}$  where  $x$,  $y$,  and  $z$  are positive integers,

what is the value of the sum  $\vphantom{\frac{x\sqrt{y}}{z}}x+y+z$ ?

______________________________________

$a\quad=\quad-\sqrt{\frac{16}{44}}\quad=\quad -\frac{4}{2\sqrt{11}}\quad=\quad\frac{-2}{\sqrt{11}}\\~\\ b\quad=\quad\sqrt{\frac{(2+\sqrt{5})^2}{11}}\quad=\quad\frac{2+\sqrt{5}}{\sqrt{11}}\\~\\~\\ (a+b)^3\,=\,\Big(\frac{-2}{\sqrt{11}}+\frac{2+\sqrt{5}}{\sqrt{11}}\Big)^3\\~\\ (a+b)^3\,=\,\Big(\frac{-2+2+\sqrt{5}}{\sqrt{11}}\Big)^3\\~\\ (a+b)^3\,=\,\Big(\frac{\sqrt{5}}{\sqrt{11}}\Big)^3\\~\\ (a+b)^3\,=\, \frac{\sqrt{5}}{\sqrt{11}} \cdot\frac{\sqrt{5}}{\sqrt{11}}\cdot\frac{\sqrt{5}}{\sqrt{11}} \\~\\ (a+b)^3\,=\, \frac{5\sqrt{5}}{11\sqrt{11}} \\~\\ (a+b)^3\,=\, \frac{5\sqrt{5}}{11\sqrt{11}}\cdot\frac{\sqrt{11}}{\sqrt{11}} \\~\\ (a+b)^3\,=\, \frac{5\sqrt{55}}{121}$

Now it is in the form  $\frac{x\sqrt{y}}{z}$  where  x,  y,  and  z  are positive integers.

x + y + z  =  5 + 55 + 121  =  181

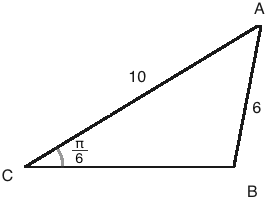
By the Law of Sines:

$\frac{\sin B}{10}\,=\,\frac{\sin( \frac{\pi}{6})}{6}\\~\\ \sin B\,=\,\frac{10\sin( \frac{\pi}{6})}{6}\\~\\ \sin B\,=\,\frac56\\~\\ B\,\approx\,56.44°\qquad\text{or}\qquad B\,\approx\,123.56°$

Both options are valid in this case because neither make the current sum of the angles exceed  180° .

the first possible value of  BC  +  the second possible value of  BC  =  $(5\sqrt3+\sqrt{11})+(5\sqrt3-\sqrt{11})$

the first possible value of  BC  +  the second possible value of  BC  =  $10\sqrt3$

Let the unknown scale factor  =  s

The sum of the angle measures in a triangle  =  180°

4s + 12s + 14s  =  180°

30s  =  180°

s  =  6°

measure of the smallest angle  =  4s  =  4(6°)  =  24°

f(x)  =  2x - 3

f(5)  =  2(5) - 3

f(5)  =  7

g( f(5) - 1 )   =   g( 7 - 1 )  =  g(6)

g(x)  =  x + 1

g(6)  =  6 + 1

g(6)  =  7

Altogether...

g( f(5) - 1 )   =   g( 7 - 1 )  =  g(6)  =  7

Great!!