Second one:
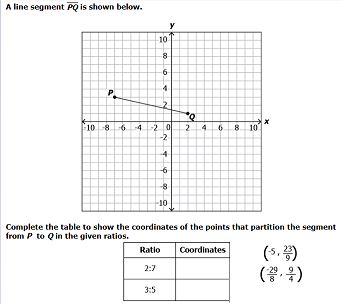
point P = (-7, 3)
point Q = (2, 1)
| _____Ratio_____ | Coordinates | |
| 2:7 | x-coordinate = \(-7+\frac{2}{2+7}\cdot|-7-2|\,=\,-7+\frac29\cdot9\,=\,-7+2\,=\,-5\) y-coordinate = \(3-\frac{2}{2+7}\cdot|3-1|\,=\,3-\frac29\cdot2\,=\,3-\frac49\,=\,\frac{23}{9}\) |
|
| 3:5 | x-coordinate = \(-7+\frac{3}{3+5}\cdot|-7-2|\,=\,-7+\frac38\cdot9\,=\,-7+\frac{27}{8}\,=\,-\frac{29}{8}\) y-coordinate = \(3-\frac{3}{3+5}\cdot|3-1|\,=\,3-\frac38\cdot2\,=\,3-\frac34\,=\,\frac94\) |
It looks like you have found the same coordinates out to the side? ![]()
Let a, b, c, and d be real numbers such that a > b and c > d .
\(\text{__________________________________________________________________________________}\)
(A) a + c > b + d
We know.....
a > b_____and_____c > d
Add d to both sides of the first inequality.
a + d > b + d
If we substitute c for d on the left side it will make the left side bigger,
and the inequality will still be true. So it is always true that
a + c > b + d
\(\text{__________________________________________________________________________________}\)
(B) 2a + 3c > 2b + 3d
| a > b | _____and_____ | c > d |
| 2a > 2b | and | 3c > 3d |
By the same logic from part (A), we can conclude that it is also true that 2a + 3c > 2b + 3d
\(\text{__________________________________________________________________________________}\)
(C) a - c > b - d
Counterexample: Let a = 2 , b = 1 , c = 2 , d = 1
a > b and c > d but it is not true that a - c > b - d because 2 - 2 > 1 - 1 is not true.
\(\text{__________________________________________________________________________________}\)
(D) ac > bd
Counterexample: Let a = 5 , b = 1 , c = -1 , d = -2
a > b and c > d but it is not true that ac > bd because (5)(-1) > (1)(-2) is not true.
\(\text{__________________________________________________________________________________}\)
(E) a2 + c2 > b2 + d2
Counterexample: Let a = 2 , b = -5 , c = 2 , d = 1
a > b and c > d but it is not true that a2 + c2 > b2 + d2 because 22 + 22 > (-5)2 + 12 is not true.
\(\text{__________________________________________________________________________________}\)
(F) a3 + c3 > b3 + d3
If a > b then | a3 | > | b3 | and a3 > b3
If c > d then | c3 | > | d3 | and c3 > d3
By the same logic from part (A) , we can conclude that it is also true that a3 + c3 > b3 + d3
Let y = x4 - 2x2
\(y\,=\,x^4-2x^2\\~\\ \frac{dy}{dx}\,=\,\frac{d}{dx}x^4-\frac{d}{dx}2x^2\\~\\ \frac{dy}{dx}\,=\,4x^3-4x\)
Now let's find what values of x make \(\frac{dy}{dx}\) be 0
\(0\,=\,4x^3-4x\\~\\ 0\,=\,4x(x^2-1) \)
Set each factor equal to zero and solve for x
\(\begin{array} {lcl} 4x=0&\qquad\text{or}\qquad &x^2-1=0\\~\\ x=0&\text{or}&x^2=1\\~\\ &&x=1\quad\text{or}\quad x=-1 \end{array}\)
These are the x values of all the critical points.
We can look at a graph to determine which is the minimum:
https://www.desmos.com/calculator/vvl7egtes1
We can see that the minumum occurs when x = 1 and when x = -1
When x = ±1 , x2 = 1
And when x2 = 1 ,
y = x4 - 2x2 = (x2)2 - 2x2 = (1)2 - 2(1) = -1
So the minumum value of y is -1