heureka

CPhill, thank you very much

Triangle $ABC$ is inscribed in equilateral triangle $PQR$, as shown.

If $PC = 3$, $BP = CQ = 2$, and $\angle ACB = 90^\circ$, then compute $AQ$.

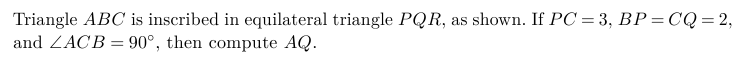
Let u = BC

Let v = CA

Let w = AB

Let x = AQ

Let PQ = PR = RQ = 5

Let BR = PR - BP \(= 5-2=3\)

Let AR = RQ - AQ \(= 5 - x\)

Using the Law of Cosines:

\(\begin{array}{|rcll|} \hline u^2 &=& BP^2 + PC^2 - 2\cdot BP \cdot PC\cdot \cos(60^{\circ}) \quad & | \quad 2\cdot \cos(60^{\circ}) = 2\cdot \frac12 = 1 \\ u^2 &=& BP^2 + PC^2 - BP \cdot PC \quad & | \quad BP =2 \quad PC = 3 \\ u^2 &=& 2^2 + 3^2 - 2 \cdot 3 \\ \mathbf{u^2} & \mathbf{=} & \mathbf{2^2 + 3^2 - 6} \\ \hline \end{array}\)

Using the Law of Cosines again:

\(\begin{array}{|rcll|} \hline v^2 &=& CQ^2 + AQ^2 - 2\cdot CQ \cdot AQ\cdot \cos(60^{\circ}) \quad & | \quad 2\cdot \cos(60^{\circ}) = 2\cdot \frac12 = 1 \\ v^2 &=& CQ^2 + AQ^2 - CQ \cdot AQ \quad & | \quad CQ =2 \quad AQ = x \\ \mathbf{v^2} & \mathbf{=} & \mathbf{2^2 + x^2 - 2x} \\ \hline \end{array}\)

Using the Law of Cosines again:

\(\begin{array}{|rcll|} \hline w^2 &=& BR^2 + AR^2 - 2\cdot BR \cdot AR\cdot \cos(60^{\circ}) \quad & | \quad 2\cdot \cos(60^{\circ}) = 2\cdot \frac12 = 1 \\ w^2 &=& BR^2 + AR^2 - BR \cdot AR \quad & | \quad BR =3 \quad AR = 5-x \\ \mathbf{w^2} & \mathbf{=} & \mathbf{3^2 + (5-x)^2 - 3 \cdot (5-x)} \\ \hline \end{array}\)

Using Pythagoras' theorem:

\(\begin{array}{|rcll|} \hline u^2+v^2&=& w^2 \\ (2^2 + 3^2 - 6) + (2^2 + x^2 - 2x) &=& 3^2 + (5-x)^2 - 3 \cdot (5-x) \\ 2^2 + \not{3^2} - 6 + 2^2 + x^2 - 2x &=& \not{3^2} + (5-x)^2 - 3 \cdot (5-x) \\ 2^2 - 6 + 2^2 + x^2 - 2x &=& (5-x)^2 - 3 \cdot (5-x) \\ 2 + x^2 - 2x &=& (5-x)^2 - 3 \cdot (5-x) \\ 2 + \not{x^2} - 2x &=& 25 - 10x + \not{x^2} -15+3x \\ 2 - 2x &=& 25 - 10x -15+3x \\ 2 - 2x &=& 10 - 7x \\ 5x &=& 8 \\ x &=& \frac85 \\ \mathbf{x} & \mathbf{=} & \mathbf{1.6} \\ \hline \end{array}\)

AQ is 1.6

Hallo asinus,

aus den Additionstheoremen lassen sich Identitäten ableiten,

mit deren Hilfe die Summe zweier trigonometrischer Funktionen als Produkt dargestellt werden kann:

\(\begin{array}{|rcll|} \hline \sin(u) + \sin(v) = 2\cdot \sin(\frac{u+v}{2})\cdot \cos(\frac{u-v}{2}) \\ \hline \end{array}\)

Dank dieser Faktorisierung geht der Ansatz zur Lösung recht einfach, doch die Lösungenmenge zu bestimmen

ist doch recht mühsam:

\(\begin{array}{|lrcll|} \hline &\sin(3y)+\sin(2y+ \frac{\pi}{3} ) &=& 0 \\\\ &\sin(3y)+\sin(2y+ \frac{\pi}{3}) = 2\cdot \sin\left(\frac{5y+\frac{\pi}{3}}{2}\right)\cdot \cos\left(\frac{y- \frac{\pi}{3}}{2}\right) &=& 0\\ & 2\cdot \sin\left(\frac{5y+\frac{\pi}{3}}{2}\right)\cdot \cos\left(\frac{y- \frac{\pi}{3}}{2}\right) &=& 0 & |~ : 2 \\ &\underbrace{\sin\left(\frac{5y+\frac{\pi}{3}}{2}\right)}_{=0}\cdot \underbrace{\cos\left(\frac{y- \frac{\pi}{3}}{2}\right)}_{=0} &=& 0 \\\\ (1) & \sin\left(\frac{5y+\frac{\pi}{3}}{2}\right) &=& 0 \\ & \Rightarrow \text{Lösungenmenge für } y \\ (2) & \cos\left(\frac{y- \frac{\pi}{3}}{2}\right) &=& 0 \\ & \Rightarrow \text{weitere Lösungenmenge für } y \\ \hline \end{array}\)

Find the remainder when r^13 + 1 is divided by r-1.

Geometric sequence:

\(\begin{array}{|rcll|} \hline \displaystyle 1+r+r^2+r^3+r^4+\ldots +r^{12} &=& \displaystyle\frac{r^{13}-1}{r-1} \\\\ \displaystyle 1+r+r^2+r^3+r^4+\ldots +r^{12} &=& \displaystyle\frac{r^{13}}{r-1}- \frac{1}{r-1} \quad & | \quad + \frac{2}{r-1} \\\\ \displaystyle 1+r+r^2+r^3+r^4+\ldots +r^{12} +\frac{2}{r-1} &=& \displaystyle\frac{r^{13}}{r-1}- \frac{1}{r-1} + \frac{2}{r-1} \\\\ \displaystyle 1+r+r^2+r^3+r^4+\ldots +r^{12} +\frac{2}{r-1} &=& \displaystyle\frac{r^{13}}{r-1}+ \frac{1}{r-1} \\\\ \displaystyle 1+r+r^2+r^3+r^4+\ldots +r^{12} +\frac{\color{red}2}{r-1} &=& \displaystyle\frac{r^{13}+1}{r-1} \\ \hline \end{array}\)

The remainder is 2.

The multiples of 12 and of 21 are written in order.

What is the smallest positive difference between a multiple of 12 and a multiple of 21?

The difference is \(n\cdot 21 -m \cdot 12 = d \) with \( n,m,d \in Z\) has a solution,

if the \(gcd(21,12)\) is a divider of \(d\). Or \(gcd(21,12) | d\).

The greatest common divisor  \(gcd(21,12) = 3.\)

The difference is \(n\cdot gcd(21,12)\)

so the difference is a multiple of 3

The differences are: \(0, 3, 6, 9, 12, \ldots\)

The smallest positive difference is 3.

What is the degree of the function that generates the data shown?

\(\displaystyle \begin{array}{|r|rrrrr|} \hline x & y\\ \hline -3 & 159 \\ & & -130 \\ -2 & 29 & & 100 \\ & & -30 & & -72 \\ -1 & -1 & & 28 & & 48 \\ & & -2 & & -24 & \\ 0 & -3 & & 4 & & 48 \\ & & 2 & & 24 & \\ 1 & \color{red}d_0=-1 & & 28 & & 48 \\ & & \color{red}d_1=30 & & 72 & \\ 2 & 29 & & \color{red}d_2=100 & & 48 \\ & & 130 & & \color{red}d_3=120 & \\ 3 & 159 & & 220 & & \color{red}d_4=48 \\ & & 350 & & 168 & \\ 4 & 509 & & 388 & & \\ & & 738 & & \\ 5 & 1247& & & & \\ \hline \end{array}\)

\(\displaystyle \begin{array}{|rcll|} \hline y(x) &=& \binom{x-1}{0}\cdot {\color{red}d_0 } + \binom{x-1}{1}\cdot {\color{red}d_1 } + \binom{x-1}{2}\cdot {\color{red}d_2 } + \binom{x-1}{3}\cdot {\color{red}d_3 } + \binom{x-1}{4}\cdot {\color{red}d_4 } \\\\ &=& \binom{x-1}{0}\cdot ( {\color{red}-1 } ) + \binom{x-1}{1}\cdot {\color{red}30 } + \binom{x-1}{2}\cdot {\color{red}100 } + \binom{x-1}{3}\cdot {\color{red}120 } + \binom{x-1}{4}\cdot {\color{red}48 } \\\\ &=& -1 \\ &&+~ \underbrace{30 \cdot(x-1)}_{\text{max degree } 1} \\ &&+~ \underbrace{100 \cdot\left(\frac{x-1}{2}\right)\cdot \left(\frac{x-2}{1}\right)}_{\text{max degree } 2} \\ &&+~ \underbrace{120 \cdot \left(\frac{x-1}{3}\right)\cdot \left(\frac{x-2}{2}\right)\cdot \left(\frac{x-3}{1}\right)}_{\text{max degree } 3} \\ &&+~ \underbrace{48 \cdot\left(\frac{x-1}{4}\right)\cdot \left(\frac{x-2}{3}\right)\cdot \left(\frac{x-3}{2}\right)\cdot \left(\frac{x-4}{1}\right)}_{\text{max degree } \color{red}4} \\ &=& \mathbf{2x^4-3} \\ \hline \end{array}\)

expand see WolframAlpha:

If the difference \(d_i\) is constant, so the degree of the polynomial to calculate the coefficients is \(i\).

\({\color{red}d_4}=48\) is constant, so the degree is \({\color{red}4}\)

If the difference \(d_i \) is constant, so the degree of the polynomial to calculate the sum of the coefficients is \(i+1\).

help with this diagram 

Can this identity be proven, and if so how?  π^2/6 = 1/6 (-i log(-1))^2

\(\begin{array}{|rcll|} \hline && \frac{1}{6}\cdot \Big(-i \log(-1) \Big)^2 \\ && &\small{ \begin{array}{|rcll|} \hline \log(z) &=& \ln|z| + i\underbrace{\arg(z)}_{=\arctan(\frac{b}{a}) } \quad | \quad z = a+b\cdot i \\ \log(-1) &=& \ln|-1| + i\underbrace{\arg(-1)}_{= \underbrace{\arctan\left(\frac{0}{-1}\right)}_{=-\pi} } \quad | \quad z = -1+0\cdot i \\ \log(-1) &=& \ln|-1| + i\cdot(-\pi) \\ \log(-1) &=& \ln(1) - i\cdot \pi \quad | \quad \ln(1) = 0 \\ \log(-1) &=& 0 - i\cdot \pi \\ \log(-1) &=& - i\cdot \pi \\ \hline \end{array}} \\ &=& \frac{1}{6}\cdot \Big(-i \cdot(- i\cdot \pi) \Big)^2 \\ &=& \frac{1}{6}\cdot (i^2 \cdot \pi )^2 \quad | \quad i^2 = -1 \\ &=& \frac{1}{6}\cdot (-\pi )^2 \\ &=& \frac{1}{6}\cdot \pi ^2 \\ &=& \dfrac{\pi ^2}{6} \\ \hline \end{array}\)

What is the value of x and y 

76x + 49y = 474.25

54x + 37y = 346.25 

\(\begin{array}{|rcl|rcl|} \hline x&=& \displaystyle \dfrac{ \begin{vmatrix} 474.25 & 49 \\ 346.25 & 37 \end{vmatrix} } { \begin{vmatrix} 76 & 49 \\ 54 & 37 \end{vmatrix} } \quad & \quad y&=& \displaystyle \dfrac{ \begin{vmatrix} 76 & 474.25 \\ 54 & 346.25 \end{vmatrix} } { \begin{vmatrix} 76 & 49 \\ 54 & 37 \end{vmatrix} } \\\\ x&=& \displaystyle \dfrac{474.25\cdot 37-346.25\cdot 49} { 76\cdot 37-54\cdot 49 } \quad & \quad y&=& \displaystyle \dfrac{ 76\cdot 346.25- 54\cdot 474.25 } { 76\cdot 37-54\cdot 49 } \\\\ x&=& \displaystyle \dfrac{581} { 166 } \quad & \quad y&=& \displaystyle \dfrac{705.5} { 166 } \\\\ x&=& \displaystyle 3.5 \quad & \quad y&=& \displaystyle 4.25 \\ \hline \end{array} \)

Ich schaffe den Beweis folgender Induktion nicht:

\(\displaystyle\sum_{k=n}^{2n-1} \frac{1}{k} = \displaystyle\sum_{k=1}^{2n-1} \frac{{(-1)}^{k+1}}{k} \)

Für alle \(n \ge 1\)

Induktionsanfang:

\(n = 1:\)   linke Seite: \(\frac{1}{1} = 1 \)

                rechte Seite:   \(\frac{(-1)^2}{1} = 1\)

Für \(n=1 \) sind beide Seiten gleich!

Induktionsschluss:

\(n+1:\)

\(\begin{array}{|rcll|} \hline && \displaystyle\sum_{k=n+1}^{2(n+1)-1} \frac{1}{k} \\\\ &=& \displaystyle\sum_{k=n+1}^{2n+2-1} \frac{1}{k} \\\\ &=& \displaystyle\sum_{k=n+1}^{2n+1} \frac{1}{k} \\\\ &=& \displaystyle\sum_{k=n}^{2n-1} \left(\frac{1}{k} \right) -\frac{1}{n} +\frac{1}{2n} + \frac{1}{2n+1} \\\\ &\overset{I.A.}{=}& \displaystyle \sum_{k=1}^{2n-1} \left(\frac{{(-1)}^{k+1}}{k}\right) -\frac{1}{n} +\frac{1}{2n} + \frac{1}{2n+1} \\\\ &=& \displaystyle \sum_{k=1}^{2n-1} \left(\frac{{(-1)}^{k+1}}{k}\right) -\frac{1}{n}\left(1-\frac{1}{2}\right) + \frac{1}{2n+1} \\\\ &=& \displaystyle \sum_{k=1}^{2n-1} \left(\frac{{(-1)}^{k+1}}{k}\right) -\frac{1}{2n} + \frac{1}{2n+1} \\\\ &=& \displaystyle \sum_{k=1}^{2n-1} \left(\frac{{(-1)}^{k+1}}{k}\right) +\frac{(-1)^{2n+1}}{2n} + \frac{(-1)^{2n+1+1}}{2n+1} \\\\ &=& \displaystyle \sum_{k=1}^{2n} \left(\frac{{(-1)}^{k+1}}{k}\right) + \frac{(-1)^{2n+1+1}}{2n+1} \\\\ &=& \displaystyle \sum_{k=1}^{2n+1} \left(\frac{{(-1)}^{k+1}}{k}\right) \\\\ &=& \displaystyle \sum_{k=1}^{2n+2-1} \left(\frac{{(-1)}^{k+1}}{k}\right) \\\\ &=& \displaystyle \sum_{k=1}^{2(n+1)-1} \left(\frac{{(-1)}^{k+1}}{k}\right) \quad \checkmark \\\\ \hline \end{array}\)