heureka

A circle centre O and radius 2cm is inscribed in an equilateral triangle ABC and touches the side BC at N. What is AN?

$$\\ \small{\text{when~ $ h = \overline{AN} $~ and one side is a}}\\\\ \qquad \tan{(60\ensurement{^{\circ}})} = \dfrac{h}{\frac{a}{2}} \qquad \tan{(30\ensurement{^{\circ}})} = \dfrac{r}{\frac{a}{2}} \\ \\ \dfrac{a}{2} = \dfrac{h}{ \tan{(60\ensurement{^{\circ}})} } = \dfrac{r}{ \tan{(30\ensurement{^{\circ}})} }\\\\\\ h= r\cdot \dfrac{ \tan{(60\ensurement{^{\circ}})} }{ \tan{(30\ensurement{^{\circ}})} } \small{\text{$ \qquad \tan{(60\ensurement{^{\circ}})} = \sqrt{3} \qquad \tan{(30\ensurement{^{\circ}})} = \dfrac{\sqrt{3} }{3} $}} \\\\\\ h= r\cdot \dfrac{ \sqrt{3}}{ \frac{\sqrt{3} }{3} }\\\\\\ h= 3\cdot r\\\\ h= 3\cdot 2~\text{cm}\\\\ h=6~\text{cm}\\\\ \mathbf{\overline{AN} = 6~\text{cm}}$$

Der Stern Alpha Centauri ist lt. Wiki 4,367 Lichtjahre von der Sonne entfernt. Das Raumschiff Helios 1 hat lt. Wiki eine Geschwindigkeit von 252792 km/h. Wie lange würde die Reise mit Helios 1 von der Sonne zum Stern Alpha Centauri dauern?

$$\small{\text{ $ \begin{array}{lll} $Die Lichtgeschwindigkeit ist$& c = 299 792 458 ~\dfrac{m}{ s } \\\\ $Die Flugzeit in Jahren berechnet sich zu $& \left(c\cdot 3,6~\dfrac{km}{Lh.}\right) \cdot \dfrac{4,367~ Lj.}{252792 ~\dfrac{km}{h}}= 299 792 458 ~\cdot 3,6 \cdot \dfrac{4,367}{252792 } = 18644,17 ~$ Jahre $\\ \end{array} $}}\\\\$$

cos(300) is equal to sin(?)

$$\small{ \cos{(300\ensurement{^{\circ}})} \text{ is equal to } \sin{(90\ensurement{^{\circ}}-300\ensurement{^{\circ}} )} = \sin{(-210\ensurement{^{\circ}} )} = \sin{(-210\ensurement{^{\circ}} + 360 \ensurement{^{\circ}} )} =\sin{(150 \ensurement{^{\circ}} } )} }$$

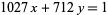
(gcd = greatest common divisor)

1. There is only a solution when gcd( 1027, 712 ) = 1 or in other words 1027 and 712 are relatively prime.

2. Using the Euclidian algorithm to calcutate gcd(1027,712)

$$\small{ \begin{array}{|r|r|r|r|} \hline &&&\\ a & b & q& r \\ \hline &&&\\ 1027 & 712 & 1 & 315 \\ 712 & 315 & 2 & 82 \\ 315 & 82 & 3 & 69 \\ 82 & 69 & 1 & 13 \\ 69 & 13 & 5 &4 \\ 13 & 4 &3 & \textcolor[rgb]{1,0,0}{1} \\ 4 & 1 & 4 & 0 \\ &&&\\ \hline \end{array} }$$

The greatest common divisor gcd(1027,712) $$\textcolor[rgb]{1,0,0}{=1}$$

and we can go on

3. Using Extended Euclidean algorithm to calculate the first solution

$$\small{ \begin{array}{|r|r|r|r||r|r|} \hline &&&&&\\ a & b & q& r &x&y\\ \hline &&&&&\\ 1027 & 712 & 1 & 315 & \textcolor[rgb]{1,0,0}{-165} & 73 - 1 (-165) = \textcolor[rgb]{1,0,0}{238}\\ 712 & 315 & 2 & 82 & 73 & -19 - 2\cdot 73 = -165\\ 315 & 82 & 3 & 69 & -19 & 16 -3(-19) = 73\\ 82 & 69 & 1 & 13 & 16 & -3 -1\cdot 16 = -19\\ 69 & 13 & 5 &4 & - 3 & 1 -5(-3) = 16\\ 13 & 4 &3 & 1 & 1 & 0 - 3\cdot 1 = -3 \\ 4 & 1 & 4 & 0 & 0 & 0\cdot 4 + 1 = 1\\ &&&&&\\ \hline \end{array} }$$

$$\small{\text{ The first solution is $ (-165,238) \qquad 1027 \cdot (\textcolor[rgb]{1,0,0}{ -165} ) + 712 \cdot \textcolor[rgb]{1,0,0}{238} = 1 $}}\\\\$$

4. All Solutions:

$$\small{\text{$ \begin{array}{lcl} \boxed{ a\cdot x + b \cdot y = 1 }\\\\ \mathrm{First~ solution~~} (x_0,~ y_0)\\ \mathrm{All~ solutions~~} \left(x_0+\dfrac{z\cdot b}{ gcd(a,b) } ,~ y_0 - \dfrac{z\cdot a}{ gcd(a,b) }\right)\\ \end{array} $}}\\\\$$

$$\small{\text{$ \begin{array}{lcl} \boxed{ 1027\cdot x + 712 \cdot y = 1 }\\\\ \mathrm{First~ solution~~} (x_0=-165,~ y_0=238)\\ \mathrm{All~ solutions~~} \left(-165+\dfrac{z\cdot 712}{ 1 } ,~ 238 - \dfrac{z\cdot 1027}{ 1 }\right)\\ \end{array} $}}\\\\$$

we have:

$$\small{\text{$ \begin{array}{lcl} \left\{~\left(~ -165 + 712\cdot z,~ 238 - 1027\cdot z\right)~|~z \in Z ~ \right\} \\ \end{array} $}}\\\\$$

what is b in

  3            2

'''''''''''''=''''''''''

3b+4      b - 4

$$\small{ \begin{array}{rll} \dfrac{3}{3b+4} &=& \dfrac{2}{b-4} \\\\ \dfrac{3b+4}{3} &=& \dfrac{b-4}{2} \\\\ b + \dfrac43 &=& \dfrac{b}{2} - 2 \\\\ \dfrac{b}{2} &=& - 2 - \dfrac43 \\\\ \dfrac{b}{2} &=& -\dfrac{10}3 \\\\ b &=& -\dfrac{20}{3}\\\\ b &=& -6\dfrac{2}{3}\\\\ \end{array} }$$

show me the process of solving (1-cot200)(1-cot25)

$$\small{ \text{$ \begin{array}{rcl} \left[ 1 - \cot{(200\ensurement{^{\circ}})} ] \cdot [ 1 - \cot{(25\ensurement{^{\circ}})} \right]\\\\ &=& \left[ 1 - \dfrac { 1 } { \tan{ ( 200\ensurement{^{\circ}} ) } } \right] \cdot \left[ 1 - \dfrac { 1 } { \tan{ ( 25\ensurement{^{\circ}} ) } } \right]\\\\ &=& \left[ \dfrac { \tan{ ( 200\ensurement{^{\circ}} ) } - 1 } { \tan{ ( 200\ensurement{^{\circ}} ) } } \right] \cdot \left[ \dfrac { \tan{ ( 25\ensurement{^{\circ}} ) } - 1 } { \tan{ ( 25\ensurement{^{\circ}} ) } } \right]\\\\ &=& \dfrac { \left[\tan{ ( 200\ensurement{^{\circ}} ) } - 1\right]\cdot \left[ \tan{ ( 25\ensurement{^{\circ}} ) } - 1 \right] } { \tan{ ( 200\ensurement{^{\circ}} ) }\cdot \tan{ ( 25\ensurement{^{\circ}} ) } }\\\\ &=& \dfrac { \tan{ ( 200\ensurement{^{\circ}} ) }\cdot \tan{ ( 25\ensurement{^{\circ}} ) } - \tan{ ( 200\ensurement{^{\circ}} ) } - \tan{ ( 25\ensurement{^{\circ}} ) } +1 } { \tan{ ( 200\ensurement{^{\circ}} ) }\cdot \tan{ ( 25\ensurement{^{\circ}} ) } }\\\\ &=& \dfrac { \tan{ ( 200\ensurement{^{\circ}} ) }\cdot \tan{ ( 25\ensurement{^{\circ}} ) } - \left[ \tan{ ( 200\ensurement{^{\circ}} ) } + \tan{ ( 25\ensurement{^{\circ}} ) } \right] +1 } { \tan{ ( 200\ensurement{^{\circ}} ) }\cdot \tan{ ( 25\ensurement{^{\circ}} ) } }\\\\ \end{array} $}}$$

$$\\\small{ \text{Formula: $ \begin{array}{rcl} &&\\ &&\\ &&\\ &&\\ \boxed{ \tan{ (200\ensurement{^{\circ}}+25\ensurement{^{\circ}} ) } = \dfrac { \tan{ ( 200\ensurement{^{\circ}} ) } + \tan{ ( 25\ensurement{^{\circ}} ) } } { 1 - \tan{ ( 200\ensurement{^{\circ}} ) } \cdot \tan{ ( 25\ensurement{^{\circ}} ) } } \qquad \tan{ (200\ensurement{^{\circ}}+25\ensurement{^{\circ}} ) } = \tan{ (225\ensurement{^{\circ}} ) } = \tan{ (180\ensurement{^{\circ}}+45\ensurement{^{\circ}} ) } = \tan{ (45\ensurement{^{\circ}} ) } = 1 } \end{array} $}} \\\\ \small{ \text{$ \begin{array}{rcl} 1 &=& \dfrac { \tan{ ( 200\ensurement{^{\circ}} ) } + \tan{ ( 25\ensurement{^{\circ}} ) } } { 1 - \tan{ ( 200\ensurement{^{\circ}} ) } \cdot \tan{ ( 25\ensurement{^{\circ}} ) } }\\\\ 1 - \tan{ ( 200\ensurement{^{\circ}} ) } \cdot \tan{ ( 25\ensurement{^{\circ}} ) } &=& \tan{ ( 200\ensurement{^{\circ}} ) + \tan{ ( 25\ensurement{^{\circ}} ) } } \\\\ \end{array} $}}$$

$$\small{ \text{$ \begin{array}{rcl} \left[ 1 - \cot{(200\ensurement{^{\circ}})} ] \cdot [ 1 - \cot{(25\ensurement{^{\circ}})} \right] &=& \dfrac { \tan{ ( 200\ensurement{^{\circ}} ) }\cdot \tan{ ( 25\ensurement{^{\circ}} ) } - \left[ \tan{ ( 200\ensurement{^{\circ}} ) } + \tan{ ( 25\ensurement{^{\circ}} ) } \right] +1 } { \tan{ ( 200\ensurement{^{\circ}} ) }\cdot \tan{ ( 25\ensurement{^{\circ}} ) } }\\\\ &=& \dfrac { \tan{ ( 200\ensurement{^{\circ}} ) }\cdot \tan{ ( 25\ensurement{^{\circ}} ) } - \left[ 1 - \tan{ ( 200\ensurement{^{\circ}} ) } \cdot \tan{ ( 25\ensurement{^{\circ}} ) } \right] +1 } { \tan{ ( 200\ensurement{^{\circ}} ) }\cdot \tan{ ( 25\ensurement{^{\circ}} ) } }\\\\ &=& \dfrac { \tan{ ( 200\ensurement{^{\circ}} ) }\cdot \tan{ ( 25\ensurement{^{\circ}} ) } -1 + \tan{ ( 200\ensurement{^{\circ}} ) } \cdot \tan{ ( 25\ensurement{^{\circ}} ) } +1 } { \tan{ ( 200\ensurement{^{\circ}} ) }\cdot \tan{ ( 25\ensurement{^{\circ}} ) } }\\\\ \end{array} $}}$$

$$\small{ \text{$ \begin{array}{rcl} \left[ 1 - \cot{(200\ensurement{^{\circ}})} ] \cdot [ 1 - \cot{(25\ensurement{^{\circ}})} \right] &=& \dfrac { \tan{ ( 200\ensurement{^{\circ}} ) }\cdot \tan{ ( 25\ensurement{^{\circ}} ) } + \tan{ ( 200\ensurement{^{\circ}} ) } \cdot \tan{ ( 25\ensurement{^{\circ}} ) } } { \tan{ ( 200\ensurement{^{\circ}} ) }\cdot \tan{ ( 25\ensurement{^{\circ}} ) } }\\\\ &=& 2\cdot \dfrac { \tan{ ( 200\ensurement{^{\circ}} ) }\cdot \tan{ ( 25\ensurement{^{\circ}} ) } } { \tan{ ( 200\ensurement{^{\circ}} ) }\cdot \tan{ ( 25\ensurement{^{\circ}} ) } }\\\\ \mathbf{ \left[ 1 - \cot{(200\ensurement{^{\circ}})} ] \cdot [ 1 - \cot{(25\ensurement{^{\circ}})} \right] }&\mathbf{ =}& \mathbf{2 } \end{array} $}}$$

Factor 

$$\\4(6x+8)+(3x^2+4x)\\\\ =4(6x+8)+x(3x+4)\\\\ =4\cdot 2(3x+4) + x(3x+4)\\\\ =8(3x+4) + x(3x+4)\\\\ =(3x+4)(8 + x)$$

Simplify  Express your answer in simplest radical form in terms of .

$$\boxed{~~ \text{Formula: } \sqrt[n]{a\cdot b} = \sqrt[n]{a}\cdot \sqrt[n]{b} ~~}$$

$$\root 3 \of {x \root 3 \of {x \root 3 \of {x \sqrt{x}}}} \\\\ = \root 3 \of {x} \cdot \root 3 \of {\root 3 \of {x \root 3 \of {x \sqrt{x}}}}\\\\ = \root 3 \of {x} \cdot \root 9 \of {x \root 3 \of {x \sqrt{x}}}\\\\ = \root 3 \of {x} \cdot \root 9 \of {x} \cdot \root 9 \of {\root 3 \of {x \sqrt{x}}}\\\\ = \root 3 \of {x} \cdot \root 9 \of {x} \cdot \root 27 \of {x \sqrt{x}}\\\\ = \root 3 \of {x} \cdot \root 9 \of {x} \cdot \root 27 \of {x} \cdot \root 27 \of {\sqrt{x}}\\\\ = \root 3 \of {x} \cdot \root 9 \of {x} \cdot \root 27 \of {x} \cdot \root 54 \of {x}\\\\ = x^{\frac13} \cdot x^{\frac19} \cdot x^{\frac1{27}} \cdot x^{\frac1{54}}\\\\ = x^{\frac13+\frac19+\frac1{27}+ \frac1{54}}\\\\ = x^{\frac13 \cdot \frac{18}{18} +\frac19 \cdot \frac{6}{6} +\frac1{27} \cdot \frac{2}{2} + \frac1{54}}\\\\ =x^{\frac{18+6+2+1}{54} } \\\\$$

$$\\=x^{\frac{27}{54}}\\\\ =x^{\frac{1}{2} } \\\\ \mathbf{= \sqrt{x}}$$