hectictar

2) 

A company wants to determine the level of interest among its employees for an annual summer picnic. The company wants to survey 200 employees. What is the best way to randomly choose these 200 employees?

If we surveyed the first 200 people to enter the cafeteria, then the result might be biased because the type of person to enter the cafeteria early might be the type of person to want a picnic more. Kind of like if you wanted to determine the level of interest a school has of making math class last for twice as long, you wouldn't want to just ask the first 200 people that turn in their math test.

Randomly selecting 200 employee ID numbers would probably be the best method.

1)

A package of cookies contains 6 cookies. Each package of cookies costs $1.49.​

A function, f(x), is written to represent the cost of purchasing x packages of cookies.

What is the practical domain for the function f(x)?

I would choose "all whole numbers" because  0  should be included in the practical domain.

(You can buy  0  packages of cookies.)

The only difference between "all positive integers" and "all whole numbers" is that  0  is

included in "all whole numbers." 

Let   \(y\,=\,9^x - 3^x + 1\)

\(y\,=\,(3^2)^x - 3^x + 1\\~\\ y\,=\,3^{2x} - 3^x + 1\\~\\ y\,=\,{\color{}(3^x)}^2-{\color{}(3^x)}+1\)

Notice that this is a quadratic equation. We can let  u = 3^x  to make it clearer.

\(y\,=\,u^2-u+1\\~\\ y\,=\,u^2-u+\frac14-\frac14+1\\~\\ y\,=\,(u-\frac12)^2-\frac14+1\)      We want to find what value of  u  minimizes  y .

When the quadratic equation is in this form we can see that the minimum value of  y  occurs when...

\(u\,=\,\frac12\\~\\ 3^x\,=\,\frac12\\~\\ x\,=\,\log_3(\frac12)\)

And when   \(x\,=\,\log_3(\frac12)\) ,

  \(y\,=\,(3^x)^2-(3^x)+1\,=\,(\frac12)^2-\frac12+1\,=\,\frac34\)

By looking at a graph, we can see this is the minimum:

Let's look at  f(x)  to determine which graph is correct.

f(x)  =  \(\frac73\)x - 3

f(0)  =  \(\frac73\)(0) - 3  =  -3

Since  f(0)  =  -3, the graph of  f(x)  passes through the point  (0, 3)

So we can see that the first graph is wrong, and the second graph is correct.

We can see that...

f(0)  =  -3    and    g(0)  =  -3    so    f(0)  =  g(0)

f(3)  =  4    and    g(3)  =  4    so    f(3)  =  g(3)

So...

x = 0  is a solution to  f(x) = g(x)

x = 3  is a solution to  f(x) = g(x)

2.  Solve   5cos²(x) + 4cos(x)  =  1   if   0  ≤  x  ≤  2π

1.  Find the value of  cos( 2θ )     when     tan( θ )  =  3/4     and     π  <  θ  <  3π/2

To use the double-angle formula for cos, let's find sin( θ ) and cos( θ ) with a sketch and the Pythagorean theorem.

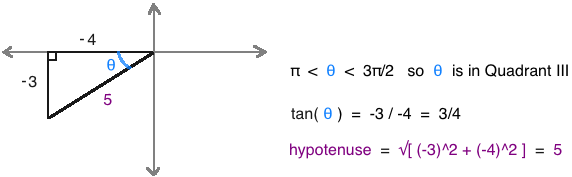
sin( θ )  =  opposite / hypotenuse  =  -3/5

cos( θ )  =  adjacent / hypotenuse  =  -4/5

What is  (f - g)(x) ?

f(x)  =  x³ - 2x² + 12x - 6

g(x)  =  4x² - 6x + 4

(f - g)(x)  =  f(x) - g(x)         Substitute  (x³ - 2x² + 12x - 6)  in for  f(x)  and substitute  (4x² - 6x + 4)  in for  g(x)

(f - g)(x)  =  (x³ - 2x² + 12x - 6) - (4x² - 6x + 4)

(f - g)(x)  =  (x³ - 2x² + 12x - 6) - (4x² - 6x + 4)

If you need to, you can simplify this by distributing the -1 outside the parenthesees and combining like terms.

What is  (f ⋅ g)(x) ?

f(x)  =  x² + 2x - 6

g(x)  =  x⁴ + 3

(f ⋅ g)(x)  =  f(x) ⋅ g(x)         Substitute  (x² + 2x - 6)  in for  f(x)  and substitute  (x⁴ + 3)  in for  g(x)

(f ⋅ g)(x)  = (x² + 2x - 6) ⋅ (x⁴ + 3)

(f ⋅ g)(x)  = (x² + 2x - 6)(x⁴ + 3)

If you need to, you can expand the right side of the equation.

Let's find  g(16) .

g(x)  =  √x

                           Plug in  16  for  x .

g(16)  =  √16

g(16)  =  4

Now let's find t(4) .

t(x)  =  3 - g(x)

                           Plug in  4  for  x .

t(4)  =  3 - g(4)

                           And  g(4)  =  √4  =  2   so we can substitute  2  in for  g(4)

t(4)  =  3 - 2

t(4)  =  1

So.....

t( g(16) )  =  t( 4 )  =  1

Notice that in both of these triangles,

AC  =  10

AB'  =  AB  =  6

m∠ACB  =  33°

However, these two are not the same triangle because

CB'  ≠  CB

m∠AB'C  ≠  m∠ABC

m∠CAB'  ≠  m∠CAB