Let the center of the circle be (h, 0)
distance between (h, 0) and (3, -2) = distance between (h, 0) and (-2, 3)
\(\begin{array}{r} \sqrt{(-2-0)^2+(3-h)^2}&\ =&\ \sqrt{(-2-h)^2+(3-0)^2}\\~\\ (-2-0)^2+(3-h)^2&=&(-2-h)^2+(3-0)^2\\~\\ (-2-0)^2-(3-0)^2&=&(-2-h)^2-(3-h)^2 \end{array}\)
Notice here that if h = 0 both sides of the equation are identical.
If you want to, you can expand both sides to also find that h = 0.
So the center of the circle is (0, 0)
And the radius = \(\sqrt{(-2-0)^2+(3-0)^2}\ =\ \sqrt{4+9}\ =\ \sqrt{13}\)
Here's a graph: https://www.desmos.com/calculator/najnuubd4e
Let n be the value of the smallest addend. Let's find the sums of the first few consecutive integers starting at n .
When the number of addends is 2 , the sum = 2n + 1
When the number of addends is 3 , the sum = 3n + 2 + 1
When the number of addends is 4 , the sum = 4n + 3 + 2 + 1
When the number of addends is 5 , the sum = 5n + 4 + 3 + 2 + 1
When the number of addends is 6 , the sum = 6n + 5 + 4 + 3 + 2 + 1
When the number of addends is 7 , the sum = 7n + 6 + 5 + 4 + 3 + 2 + 1 = 7n + 7 + 7 + 7 = 7n + 7(7 - 1)/2
When the number of addends is a , the sum = an + a(a - 1) / 2
So we want to find the integer solutions to this equation:
an + a(a - 1) / 2 = 60
I don't know how to do that........so I had to use WolframAlpha to solve it. See:
https://www.wolframalpha.com/input/?i=integer+solutions:+a*n+%2B+a(a+-+1)+%2F+2%3D60,+a%3E0
Assuming a > 1 , there are 7 different ways to express the number 60 as a sum of consecutive integers:
19 + 20 + 21 = 60
10 + 11 + 12 + 13 + 14 = 60
4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 = 60
-3 + -2 + -1 + 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 = 60
-9 + -8 + -7 + -6 + . . . + 9 + 10 + 11 + 12 + 13 + 14 = 60
-18 + -17 + -16 + . . . + 18 + 19 + 20 + 21 = 60
-59 + -58 + -57 + . . . + 59 + 60 = 60
Here's another way...
Let's extend
WZ to point A,
XY to point B,
ZY to point C,
WX to point D, and
YX to point E
Like this:
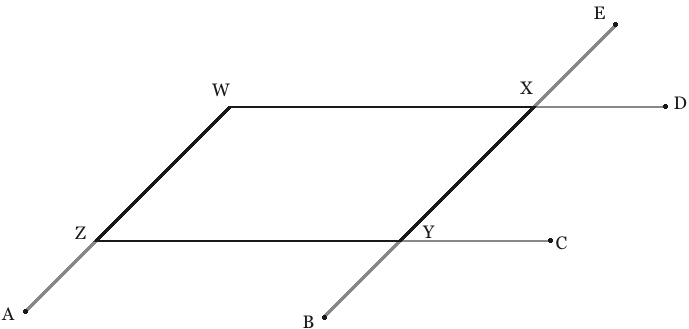
| m∠XWZ = m∠YZA | _____ | because corresponding angles are congruent. |
| m∠YZA = m∠CYB |
| because corresponding angles are congruent. |
| m∠CYB = m∠XYZ | because vertical angles are congruent. | |
| Therefore |
| |
| m∠XWZ = m∠XYZ | by the transitive property of congruence. | |
|
Likewise... |
| |
| m∠WZY = m∠XYC | because corresponding angles are congruent. | |
| m∠XYC = m∠EXD |
| because corresponding angles are congruent. |
| m∠EXD = m∠WXY | because vertical angles are congruent. | |
| Therefore |
| |
| m∠WZY = m∠WXY | by the transitive property of congruence. |
Add the two equations together to get
2a = 8b
a = 4b
Substitute this value in for a in the first given equation.
4b + (4b)b2 = 40b
4b + 4b3 = 40b
Subtract 40b from both sides of the equation.
4b3 - 36b = 0
Factor b out of the terms on the left side.
b(4b2 - 36) = 0
Factor 4b2 - 36 as a difference of squares.
b(2b + 6)(2b - 6) = 0
Set each factor equal to zero and solve for b
| b = 0 | ____or____ | 2b + 6 = 0 | ____or____ | 2b - 6 = 0 |
| 2b = -6 |
| 2b = 6 | ||
| b = -3 | b = 3 |
If b = 0 then a = 4b = 4(0) = 0 so (0, 0) is a solution.
If b = -3 then a = 4b = 4(-3) = -12 so (-12, -3) is a solution.
If b = 3 then a = 4b = 4(3) = 12 so (12, 3) is a solution.