1) P(x) = P(0) + P(1)x + P(2)x2
| Plug in 1 for x to get: |
| |
| P(1) = P(0) + P(1) + P(2) | __ | Subtract P(1) from both sides of the equation |
| 0 = P(0) + P(2) |
| Subtract P(2) from both sides |
| -P(2) = P(0) |
|
Plug in -1 for x to get:
| P(-1) = P(0) - P(1) + P(2) |
__ | Since P(-1) = 1 we can substitute 1 in for P(-1) |
| 1 = P(0) - P(1) + P(2) | Add P(1) to both sides and subtract 1 from both sides. | |
| P(1) = P(0) + P(2) - 1 |
| Substitute 0 in for P(0) + P(2) |
| P(1) = -1 |
Plug in 2 for x to get:
| P(2) = P(0) + 2P(1) + 4P(2) | __
| Substitute -1 in for P(1) and subsitute -P(2) in for P(0) |
| P(2) = -P(2) + 2(-1) + 4P(2) | Simplify the right side. | |
| P(2) = 3P(2) - 2 |
| Subtract 3P(2) from both sides. |
| -2P(2) = -2 | Divide both sides by -2 | |
| P(2) = 1 |
| |
| Now we can find P(0): |
| |
| P(0) = -P(2) Substitute 1 in for P(2) | ||
| P(0) = -1 |
| |
So we have found that P(x) = -1 - x + x2
(a)
\(\sqrt{x^2+y^2}\ =\ 5\)
The solutions to this equation are all points with a distance of 5 from the origin.
So this is the equation of a circle with a radius of 5 centered at the origin.
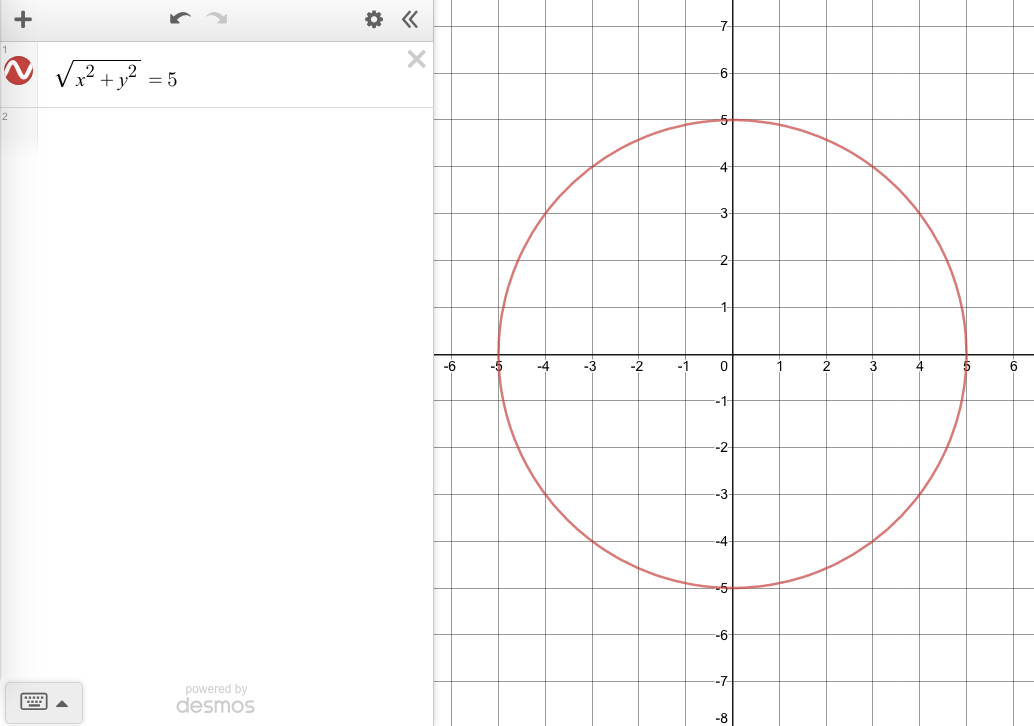
I used a little help from here: https://math.stackexchange.com/questions/518856/integral-points-on-a-circle
There is a Pythaogrean triple with a hypotenuse of 5
A triangle with side lengths 3, 4 and 5 is a Pythagorean triple. So...
From the origin, we can go over 3 units and either up or down 4 units to reach an integer solution.
From the origin, we can go over 4 units and either up or down 3 units to reach an integer solution.
From the origin, we can go over 0 units and either up or down 5 units to reach an integer solution.
From the origin, we can go over 5 units and either up or down 0 units to reach an integer solution.
Here's a graph showing all integer solutions: https://www.desmos.com/calculator/txwzj5nmt4
There are 12 integer solutions.