This video really helped me understand: https://www.youtube.com/watch?v=BZxZ_eEuJBM
If \(z=-8+15i\) then \(\overline{z}=-8-15i\)
If \(w=6-8i\) then \(\overline{w}=6+8i\)
And so...
\(\dfrac{z\overline{z}}{w\overline{w}}\ =\ \dfrac{(-8+15i)(-8-15i)}{(6-8i)(6+8i)}\ =\ \dfrac{(-8)^2-(15i)^2}{(6)^2-(8i)^2}\ =\ \dfrac{64+225}{36+64}\ =\ \dfrac{289}{100}\)
Just like CPhill found. ![]()
In order for ∠A to be the largest angle, It must be that the side formed by ∠A is the largest side. So...
| 3x < x + 9 | |
| 2x < 9 |
|
| x < \(\frac92\) |
But by the triangle inequality theorem,
| x + 9 < ( 3x ) + ( x + 4 ) | |
| x + 9 < 3x + x + 4 |
|
| 9 < 3x + 4 | |
| 5 < 3x |
|
| \(\frac53\) < x |
So in order for ∠A to be the largest angle, it must be that \(\frac53
The least possible value of n - m is \(\frac92-\frac53\ =\ \frac{27}{6}-\frac{10}{6}\ =\ \boxed{\frac{17}{6}}\)
( Here's an older answer for this question: https://web2.0calc.com/questions/geometry-question. . .#r5 )
Using the short scale definitions from the table here: https://en.wikipedia.org/wiki/Names_of_large_numbers
| 72.1 Quadrillion | = | 72.1 × 1015 | = | 72.1 × 1015 | = | 7.21 × 1016 | = | 72 100 000 000 000 000 |
| ___ | ___ | ___ | ___ | |||||
| 1000 Trillion × 72 | = | 103 × 1012 × 72 | = | 72 × 1015 | = | 7.2 × 1016 | = | 72 000 000 000 000 000 |
So 72.1 Quadrillion is pretty close to 100 Trillion × 72 but they're not exactly the same.
( If you use the long scale definitions you get 72.1 × 1024 and 72 × 1021 which are further apart.)
And neither are equal to 1072 . 1072 is 1 with 72 zeros after it.
1072 = 1 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000
I found three different possible values of d using this graph:
https://www.desmos.com/calculator/cwbrobjoav
You can turn on the different parallelograms by clicking the circle next to the name.
Here's a picture with all of them turned on:
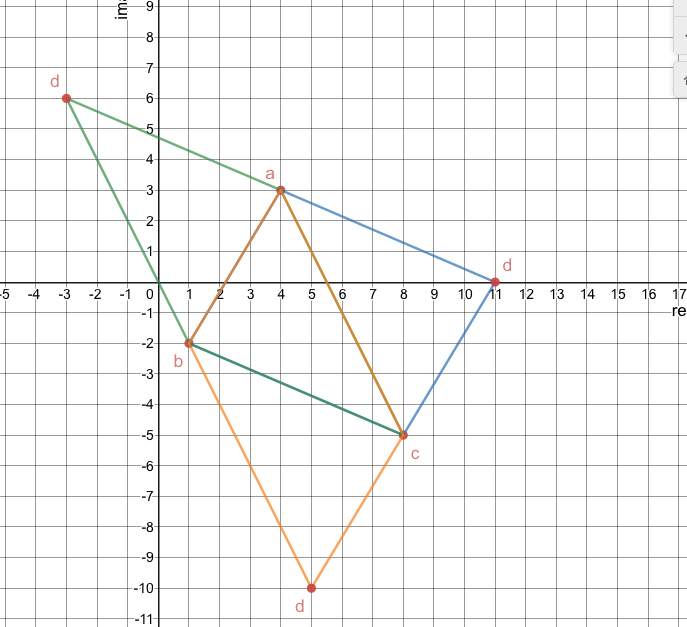
| The different possible values of d are: |
|
| -3 + 6i |
|
| 5 - 10i |
|
| 11 + 0i |