hectictar

f(x) does not pass through the point  (0, 2)

See where  (0, 2)  is on the graph:

Let's look at the next option....

f(x)  and  g(x)  have a common x-intercept. True or false?

An x-intercept is a point on the graph where  y  is  0 .

By looking at the table, we can see that when  g(x) = 0 ,  x = 2

That means an x-intercept on the graph of  g(x)  is  (2, 0)

Does  f(x)  also appear to pass through the point  (2, 0)  ?

If so, then it is true that f(x)  and  g(x)  have a common x-intercept.

f(x)  and  g(x)  have the same y-intercept. True or false?

The y-intercept is the point on the graph where  x  is  0 .

By looking at the table, we can see that when  x = 0 ,  g(x) = 2 .

That means the y-intercept on the graph of  g(x)  is  (0, 2)

Is the y-intercept the same on the graph of f(x)?

That is, does  f(x)  appear to pass through the point  (0, 2)  ?

We can use the law of sines:

\(\begin{array}{rcl} \frac{\sin A}{a}&\,=\,&\frac{\sin B}{b}\\~\\ \frac{\sin(50°)}{3}&\,=\,&\frac{\sin B}{2}\\~\\ 2\cdot\frac{\sin(50°)}{3}&\,=\,&\sin B\\~\\ \frac{2}{3}\sin(50°)&=\,&\sin B \end{array} \\ \ \\~\\ B\approx30.71°\quad\text{or}\quad B\approx149.29° \)

There are infinitely many values of B that produce the same sin value, but we only want to consider those

that are in the interval  (0, 180°)  because no angle in a triangle can have a measure outside that interval.

This is how we find those two solutions:

\(B\,=\,\arcsin(\frac{2}{3}\sin(50°))\qquad\text{or}\qquad B\,=\,180°-\arcsin(\frac{2}{3}\sin(50°))\)

But in this case,  B ≈ 149.29° can't be a solution because we already have an angle that is 50°,  and

149.29° + 50°  >  180°

So we know  B ≈ 30.71°  is the only solution for this problem. So there is only one possible triangle.

Now we can find the measure of angle  C .

C  =  180° - A - B  ≈  180° - 50° - 30.71°  ≈  99.29°

All we are missing is the length of side c. We can find it using the law of cosines.

c²  =  a² + b² - 2ab cos C

c²  ≈  3² + 2² - 2(3)(2) cos( 99.29° )

c²  ≈  13 - 12 cos( 99.29° )                  c  is a length, so take the positive sqrt of both sides

c  ≈  √[ 13 - 12 cos( 99.29° ) ]              Plug this into a calculator

c  ≈  3.865

Now we have found:

B  ≈  30.71°

C  ≈  99.29°

c  ≈  3.865

Guest, it is not true that we can always form a triangle given 2 sides and a non-included angle.

For example, let  a = 1,  b = 2,  A = 45°

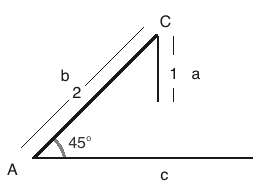
The length of side  c  is not fixed and the measure of angle  C  is not fixed.

There is still no way to exend/shorten  c  or rotate  a  so that  a  touches  c .

Side  a  is just too short to ever touch side  c .

It is also possible that two different triangles can be formed from the same given side-side-angle.

Circle \(\Gamma\) is the incircle of \(\triangle ABC\) and is also the circumcircle of \(\triangle XYZ\). The point \(X\) is on \(\overline{BC}\), the point \(Y\) is on \(\overline{AB}\), and the point \(Z\) is on \(\overline{AC}\). If \(\angle A=40^\circ\), \(\angle B=60^\circ\), and \(\angle C=80^\circ\), what is the measure of \(\angle YZX\)?

----------

Instead of calling the center of the circle  \(\Gamma\) , let's call it  G .

Y is a point on both the circle and its tangent line AB. So Y must be a point of tangency. The same goes for X.

Draw a line from G to Y and line from G to X. These form right angles with the tangent lines.

Look at quadrilateral BYGX. The sum of the angle measures in a quadrilateral  =  360° . So...

m∠YGX  =  360° - 90° - 90° - 60°  =  120°

The measure of an inscribed angle is half the measure of the central angle with the same intercepted arc.

m∠YZX  =  (1/2)(m∠YGX)  =  (1/2)(120°)  =  60°

Yep! You can use the quadratic formula to solve   -16t²  - 60t + 54  =  0   for  t , like this:

\(t \,=\, {-(-60) \,\pm \,\sqrt{(-60)^2-4(-16)(54)} \over 2(-16)}\,=\,{60\, \pm \,\sqrt{7056} \over -32}\,=\, {60 \,\pm\, 84 \over -32}\\~\\ \ \\ \begin{array}\ t\,=\,\frac{60+84}{-32}&\qquad\text{or}\qquad& t\,=\,\frac{60-84}{-32}\\~\\ t\,=\,\frac{144}{-32}&\qquad\text{or}\qquad& t\,=\,\frac{-24}{-32}\\~\\ t\,=\,-4.5&\qquad\text{or}\qquad& t\,=\,0.75 \end{array}\)

height  =  -16t²  - 60t + 54     , where  t  is the number of seconds after the ball is released

In how many seconds will the ball hit the ground?

In other words, what is  t  when the height is zero?

Plug in  0  for the height and solve for  t .

0  =  -16t²  - 60t + 54

                                             We can divide both sides of the equation by  -2

0  =  8t² + 30t - 27

                                             Let's split  30t  into two terms such that their coefficients multiply to  -216

0  =  8t² - 6t + 36t - 27

                                             Factor  2t  out of the first two terms and factor  9  out of the last two terms

0  =  2t(4t - 3) + 9(4t - 3)

                                             Factor  (4t - 3)  out of both remaining terms

0  =  (4t - 3)(2t + 9)

                                             Set each factor equal to  0  and solve for  t

We want the number of seconds after the ball is released, so we only want the positive solution.

The ball will hit the ground  0.75  seconds.

Let's get the equation into the form

(x - h)² + (y - k)²  =  r²     where the point  (h, k)  is the center of the circle and  r  is the radius.

9x² - 18x + 9y² + 36y + 44  =  0

                                                         Subtract  44  from both sides of the equation

9x² - 18x + 9y² + 36y  =  -44

                                                         Divide both sides by  9

x² - 2x + y² + 4y  =  - \(\frac{44}{9}\)

                                                         Add  1  and add  4  to both sides to complete the squares on the left side

x² - 2x + 1  +  y² + 4y + 4   =   - \(\frac{44}{9}\) + 1 + 4

                                                                         Factor both perfect square trinomials on the left side

(x - 1)²  +  (y + 2)²   =   - \(\frac{44}{9}\) + 1 + 4

                                                                         Get a common denominator to combine  - \(\frac{44}{9}\) + 1 + 4

(x - 1)²  +  (y + 2)²   =   - \(\frac{44}{9}\) + \(\frac99\) + \(\frac{36}{9}\)

(x - 1)²  +  (y + 2)²   =   \(\frac19\)

Now it is in the form     (x - h)² + (y - k)²  =  r²     and we can see that...

r²  =  \(\frac19\)

                  The radius is positive so take the positive sqrt of both sides

r  =  \(\frac13\)

Billie, a bushwalker, goes on a four day journey. She travels a certain distance on the first day, half that distance on the second day, a third that distance on the third day and a quarter of that distance on the fourth day. If the total distance is 50km, how far did she walk on the first day?

The meaning of the blue words is ambiguous. So there are multiple different interpretations of the problem. Each interpretation yields a different answer.

I think that the intended interpretation is this:

Billie, a bushwalker, goes on a four day journey. She travels a certain distance on the first day, half that distance on the second day, a third the distance traveled on the first day on the third day and a quarter of the distance traveled on the first day on the fourth day. If the total distance is 50km, how far did she walk on the first day?

There are 2 reasons why I think that is the intended interpretation:

1.  All instances of "that distance" in the problem statement would refer to the same thing.

2.  The solution would be an integer, and an integer that is divisible by 2, 3, and 4 at that.