I think this is one of those times where simplifying the problem may make it easier to understand. Mathematicians utilize this strategy all the time, and it amazes me how many times it works. Instead of considering a three-dimensional figure, let's solely focus on the base of the tetrahedron, figure PQR.
A few rules govern the existence of this triangle. Let's consider the rules one at a time. If the sidelengths of \(\triangle PQR\) can only consist of lengths of 18 or 41, then this narrows the possibilities to 4 options. The images below are not drawn to scale. The central label indicates how I will differentiate and refer to the triangles:
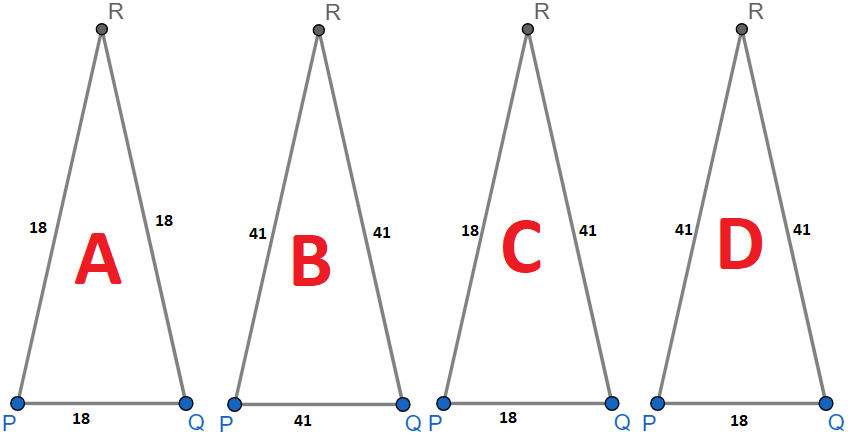
The next rule is that no face is equilateral; in other words, the triangle cannot have all sides with equal length. Since both triangle A and triangle B are equilateral in nature, these two cannot be the base of the tetrahedron.
There are no more rules given in the problem, yet there are still two triangles left as possibilities. Can we eliminate one? Yes, absolutely! Triangle C cannot be a triangle because it cannot exist. By the Triangle Inequality Theorem, the sum of the lengths of any two sides of a triangle must be greater than the length of the remaining side. The triangle fails this theorem. \(18+18\ngtr 41\). If a triangle fails the theorem, then the figure cannot be a triangle.
This leaves us with one and only one possibility: the 18-41-41 triangle. Since all the faces of this figure, known as a tetrahedron, is a triangle with the rules aforementioned, then all other faces must be an 18-41-41 triangle, too. A tetrahedron has 4 faces, so I can find the area of one base and multiply it by 4. The area of the base can be obtained with heron's formula. Doing this will get the surface area of the three-dimensional figure.
| \(SA_{\text{tetrahedron}}=4\sqrt{s(s-a)(s-b)(s-c)}\) | In heron's formula, a, b, and c are side lengths of any triangle. s is the semiperimeter. Let's find the semiperimeter first. |
| \(s=\frac{18+41+41}{2}=50\\ a=18\\ b=41\\ c=41\) | Now, substitute into heron's formula and solve. |
| \(SA_{\text{tetrahedron}}=4\sqrt{50(50-18)(50-41)(50-41)}\) | Simplify the expressions within parentheses. |
| \(SA_{\text{tetrahedron}}=4\sqrt{\textcolor{red}{50}*\textcolor{blue}{32}*\textcolor{green}{9*9}}\) | Let's try to extract all the perfect squares from this. |
| \(SA_{\text{tetrahedron}}=4\sqrt{\textcolor{red}{25*2}*\textcolor{blue}{16*2}*\textcolor{green}{9^2}}\) | We can combine the red 2 with the blue 2 to make another perfect square. |
| \(SA_{\text{tetrahedron}}=4\sqrt{5^2*4^2*9^2*2^2}\) | Let's take out all the perfect squares now! |
| \(SA_{\text{tetrahedron}}=4*\textcolor{red}{5*4}*\textcolor{blue}{9*2}\) | Now, multiply in any order you choose. I chose to multiply this way because it felt easiest. |
| \(SA_{\text{tetrahedron}}=\textcolor{red}{4}*20*\textcolor{red}{18}\) | |
| \(SA_{\text{tetrahedron}}=20*72\) | |
| \(SA_{\text{tetrahedron}}=1440\text{units}^2\) | Do not forget about those units! |
You are correct in stating that the new volume of the cylinder is 80% of the original right cylinder. Although this is a true observation, it does not answer what the value of the percent is.
However, what 80% tells you is that this is certainly a percent decrease.
| \(V_{\text{new}}=V_{old}-xV_{old}\) | I am subtraction a portion of the old volume to see what the decimal will be. Use substitution here. |
| \(V_{\text{new}}=0.8\pi r_{\text{old}}^2h_{\text{old}}\\ V_{\text{original}}=\pi r_{\text{old}}^2 h_{\text{old}}\) | |
| \(0.8\pi r_{\text{old}}^2 h_{\text{old}}=\pi r_{\text{old}}^2 h_{\text{old}}-x\pi r_{\text{old}}^2 h_{\text{old}}\) | Now, solve. I will factor. |
| \(0.8\pi r_{\text{old}}^2 h_{\text{old}}=\pi r_{\text{old}}^2 h_{\text{old}}(1-x)\) | I will divide both sides by \(\pi r^2 h\). This get's rid of a lot of the variables. |
| \(0.8=1-x\) | |
| \(-0.2=-x\) | |
| \(x=0.2\Rightarrow 20\%\text{ change}\) | The question asks for the percent change, so I convert from a decimal to a percent. |
\(\boxed{1}\hspace{3mm}y=x^2-3x+4\\ \boxed{2}\hspace{3mm}x+y=4\)
In the system of equations, the first equation is already solver for, so I can substitute its value into the second question.
| \(y=\textcolor{red}{x^2-3x+4};\\ x+\textcolor{red}{y}=4\) | Use substitution to get rid of one variable. | ||||
| \(x+\textcolor{red}{x^2-3x+4}=4\) | Combine like terms and subtract 4 from both sides. | ||||
| \(x^2-2x=0\) | Factor the GCF of the left-hand side of the equation: x. | ||||
| \(x(x-2)=0\) | Set both factors equal to 0 and solve. | ||||
| |||||
Let's substitute both possibilities for y:
| \(\boxed{2}\hspace{3mm}x+y=4\) | Let's substitute in the first possibility for x: x=0. |
| \(0+y=4\) | |
| \(y_1=4\) | |
| \(\boxed{2}\hspace{3mm}x+y=4\) | Substitute for the second option: x=2. |
| \(2+y=4\) | |
| \(y_2=2\) | |
Here are the answers in coordinate form: \((0,4)\) and \((2,2)\)
.1) It turns out that someone has already asked this question already, and I just happen to remember this post from February 27 of this year. I see no reason to make a duplicate answer.
Here is the link: https://web2.0calc.com/questions/help_80894
2a) The following equation below shows the general formula for a function that has exponential growth or decay.
\(P(t)=a*b^t\)
\(P(t)\) represents the function that yields the population of the town t years after 2010.
a = initial population of town
b = rate of exponential growth or decay
Since a is the initial population of the town, a=8500.
b, in this case, represents the portion of the population that remains as a fraction or decimal. The population begins at 100%. If the population decreases by 4.5% every year, then 100%-4.5% or 95.5% represents the percentage of the population that remains. As a decimal, this would be written as 0.955.
Now that both of this function are known, we can create an equation to find the population t years after 2010.
\(P(t)=8500(0.955)^t\)
2b) Since I have generated the equation for you, do you think that you could solve the next one? Just substitute into the formula and solve.