TheXSquaredFactor

This problem is a simple example of the application of the law of sines. The law of sines relates the sine of an angle of an oblique triangle to its opposite side length via proportions.

\(\frac{\sin A}{a}=\frac{\sin C}{c}\)

When the angle measure in given in radians, the formula for arc length is the following:

\(\text{Arc length}=r\theta\)

r = length of radius

\(\theta =\) measure of angle, in radians

Let's use this formula, then!

Just to clear up any confusion, hecticar, \(x\neq -1\). Any time a division-by-zero error arises, the entire expression is immediately deemed as undefined--no matter where. 

We have reached a problem. Do not go any further! Here is another way to think about, I guess.

Any result in the format \(\frac{x}{0}\) is given the name "undefined" because it literally does not have a meaning; it is pure nonsense; it means nothing at all. By taking the reciprocal, you are attempting to attach meaning to nonsense, which you should never do.

When many segments are named, and there is a lot of information conveyed in a succinct manner, I would suggest creating a diagram that represents the situation. The diagram below does just that:
 

What can you conclude about this diagram, and how can you apply it to the answer choices? 

Problem #1: "how close does the line 2x-5y=4 come to the point (1,5)​"

When measuring distance from a point to a line, it is important that you find the perpendicular distance. I think a diagram could be useful for this problem. I have provided you with one that encompasses this exact problem:

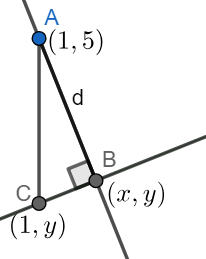
\(\overline{BC}\) is included in the equation given, \(2x-5y=4\)

d is the perpendicular distance from the desired point, A, to the line, 

I think that converting the equation into slope-intercept (y=mx+b) form is the way to go. To do this, solve for y:

When the equation is in this form, it gives us much more valuable information that standard form does. For example, we now know what the slope is. This can also allow us to find the slope of the perpendicular line because perpendicular lines are always opposite reciprocals of the original slope. 

Why would we want to find the equation of the line AB. Well, I now have a system of equations, so I can figure out where both lines intersect. As a refresher, here are the equation of both lines again. Both lines are already solved for y, so we can utilize the substitution method to figure out the intersection point.:

\(y=\frac{2}{5}x-\frac{4}{5}\\ y=-\frac{5}{2}x+\frac{15}{2}\)

Unfortuntately, these are not the nicest numbers. We now have to compute the y-coordinate. Substitute in the x-coordinate for one of the two equations.

To find the distance, just use the distance formula! This finds the distance from point A to B, which is also the closest. 

Problem #2: "how close does the circle with the radius 4 and center at (4,3) come to the point (10,3)?"

I think this question is easier to answer. The center of the circle lies on (4,3). The radius is 4 units long, so it could extend to the point (8,3), which is 2 units away from the desired point (10,3). I know this because both points lie on the same y-coordinate. 

The empirical rule (sometimes referred to as 68-95-99.7% rule) will come be handy here. This empirical rule expresses the percent of the values that are 1 to 3 standard deviations in both directions of the mean with a normal distribution:

Although the notation is sloppy, I will assume based on former questions of the same that "∑n=15[5(−2)^n−1]" translates mathematically to \(\sum_{n=1}^5[5(-2)^{n-1}]\). Please correct me, though, if this in incorrect. 

Anyway, there is neat formula that will deal with question very quickly. It is the following:

\(S_n=a_1\left(\frac{1-r^n}{1-r}\right),r\neq1\)

S_n is the sum of the geometric series

a₁ is the first term in the series

r is the common ratio

n is the number of terms in the finite geometric series

Let's use this formula to our advantage! However, there are two variables that we do not know: a₁ and  n. Let's start with a₁.The first term in the series is when n=1, so let's determine what that is. 
 

The number of terms also must be calculated:

In order for a pair of polygons to be considered similar, the polygon must meet two conditions:

1) All corresponding angles are congruent

2) The ratio of corresponding sides of both polygons is equal (also known as constant of proportionality)

Since the ratio of the side lengths is equal, we can set up a proportion to represent the equal ratios. 

Gavin, I believe you made another error here. For your application of the Pythagorean's theorem, you did the following: 

\(x^2+(2x)^2=(​2\sqrt6)^2\\ x^2+4x^2=4\cdot6\\ 5x^2=24\\\)

However, I do not understand why 2x is the representation of a leg in this equation, but you show in your diagram that it is clearly the representation of the hypotenuse's length. If you wanted to use this method to get the answer, then x and x√​3 should be the lengths. The work would look something like this:
 

\(x^2+\left(\textcolor{red}{x\sqrt{3}}\right)^2=\left(2\sqrt{6}\right)^2\\ x^2+\textcolor{red}{3}x^2=2^2*\sqrt{6}^2\\ \textcolor{red}{4}x^2=4*6\\ \textcolor{red}{4}x^2=24\)

That small error from your work makes the discrepancies highlighted in red. You can, then, solve for x and plug them in for the legs, but you can also use the method below.

The ratio of the sidelengths of the 30-60-90 special right triangle is \(1:\sqrt{3}:2\), so Pythagorean's theorem is not necessary. Of course, you can still use it if you wish. However, it is also possible to generate this answer with your knowledge of proportions.  

\(\frac{2\sqrt{6}}{2}=\frac{\text{leg}_1}{1}\\ \text{leg}_1=\sqrt{6}\)

\(\frac{2\sqrt{6}}{2}=\frac{\text{leg}_2}{\sqrt{3}}\\ \text{leg}_2=\sqrt{6}*\sqrt{3}=\sqrt{18}=3\sqrt{2} \)

Now, add them together. 

\(\left(3\sqrt{2}+\sqrt{6}\right)\text{cm}\approx 6.6921\text{cm}\) is, then, the sum of the length of the sides.