Melody

Try proof reading your questions. You have left out core info.

And only ask one question per post.

That is a very good question and maybe one I will struggle with explaining.

You have the initial interval AB

I drew 2 lines that were perpendicular to AB and therefore parallel to each other. 

I called them BC and AD   but the exact position of C and D is not set yet

The line crossed AD at 2 units.

So  the lines must go right 2 up one and left 2.    I changed that to out 4 and up one.

So now I have the rectangle aa'b'b    

going diagonally the closest way to get from A to B'  is in a straight line.

Thanks Asinus and also Builderboi 

I have another method.

This is a question where the maths is super easy but understaning the concept may be a lot more challenging.

Rule: The shortest distance between 2 points is a line.

I have reflected the line AB  around  the line x=2 to get the line A'B'

Now to go from A to any point on the doted line and then back to B ist the same as going from A to that same point and then to B'

The shortest distance from A to B' is a straight line.  The length is     \(\sqrt{4^2+1^1 }=\sqrt{17}\)

Now you can find the actual point where the distance will be least using calculus but that is definitely not easy so I did it graphically.

I let the point giving the shortest distance be G

AG=EC   drew the circle

BG=AE   drew the circle.

Point G is where the circles and the line all cross each other.

Sorry Cheesesteak, but that answer is NOT correct.   I am very pleased that you have responded though.

Take a point that is 0.3 units from the cente, now rotate that point 180 degrees to get the second point.

The two points are 0.6 units and 180 degrees apart. 

You said the 2 points had to be less than 60 degrees apart.  You have only found a small portion of the solutions

There are 12*4 = 48 favourable sets of 3 cards

52C3 = 22100 sets of 3 altogether 

So what do you think the answer is?

Hopefully all my errors are now fixed.

Yes you are right.  (I forgot about that bit)

I have made a lot of careless mistakes.

I will fix it in the morning.

It is always very pleasing when I know my answers have been examined properly.  

(Even when they are riddled with errors)

THANKS CHEESESTEAK1432  

just work outwards

g(27) = 3^27

\(f [g(27)] = f ( 3^{27} ) = log_3(3^{27})=27log_33=27\\ etc\)

It went up by 6

Initially    

S students took only spanish

C stuents took Chinese

B students took both

27 did neither.

Total number of students = S+C+B+27

The total number of 10 sudeents dropped chines but the number doing neither only went up by 4

Those 4 had to come from the Chines only group, the other 6 came from the both group.

So now there are

C-4   students doing chinese

B-6 students doing both

S+6 srtdents doing only chinese

and 31 doing neither

Total number of students =   C-4  +  B-6  +  S+6    +31 =  C+B+S+ 27

Earlier errors are now fixed.  I hope there are no more.

Question: Two points on a circle of radius 1 are chosen at random. Find the probability that the distance between the two points is at most 1.

I have spent a long time on this, I think this answer is correct.

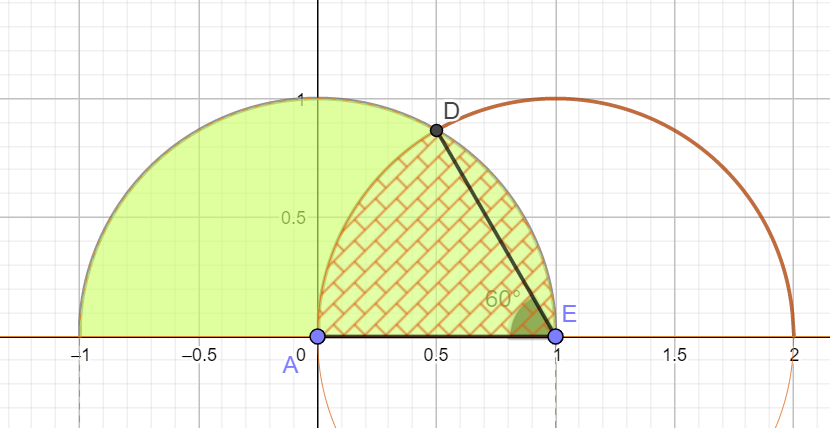
Orient your  circle so that the interval joining the 2 points that you choose is above and parallel to the diameter.

The green semicircle is the top of the original circle.

If I draw  1 unit intervals paralel to the diameter how much of semicircle will not be included.

I needed a curve 1 unit to right of the original and the area in the bricked in area indicatesw the left over.

So the prob of the points being 1 unit or less apart is the  clear green area over the whole green semicircle.

Area of Simicircle = \(\frac{\pi}{2}\)

Area of the bricked sector sector =

 \(\frac{60}{360}*\pi\\ =\frac{\pi}{6}\\\)

Area of bricked segment

\(=\frac{\pi}{6}-\frac{1}{2}*1*\sqrt{1^2-0.5^2}\\ =\frac{\pi}{6}-\frac{1}{2}*\frac{\sqrt{3}}{2}\\ =\frac{\pi}{6}-\frac{\sqrt{3}}{4}\\ =\frac{2\pi-3\sqrt3}{12}\)

Total bricked area 

\(=\frac{2\pi}{12}+\frac{2\pi}{12}-\frac{3\sqrt3}{12}\\ =\frac{4\pi-3\sqrt3}{12}\\ \)

Area on non-bricked section

\(\frac{6\pi}{12}-\frac{4\pi-3\sqrt3}{12}\\ =\frac{2\pi +3\sqrt3}{12}\\\)

Probability that the points will be less than or equal to 1 unit apart 

\(=\frac{2\pi+3\sqrt3}{12}\div \frac{\pi}{2}\\ =\frac{3\sqrt3+2\pi}{6\pi} \\ \approx 61\%\)

Hopefully I have now fixed all the errors.