https://en.wikipedia.org/wiki/Euclidean_algorithm
Examples:
The greatest common divisor of 6 and 9
= gcd(6, 9) ←The difference between 6 and 9 is 3, so replace the larger number, 9, with 3.
= gcd(6, 3) ←The difference between 6 and 3 is 3, so replace the larger number, 6, with 3.
= gcd(3, 3) ←Now the two numbers are the same. So we stop.
= 3
The greatest common divisor of 8 and 12
= gcd(8, 12)
= gcd(8, 4)
= gcd(4, 4)
= 4
The greatest common divisor of 24 and 81
= gcd(24, 81)
= gcd(24, 57)
= gcd(24, 33)
= gcd(24, 9)
= gcd(15, 9)
= gcd(6, 9)
= gcd(6, 3)
= gcd(3, 3)
= 3
To calculate the greatest common divisor of 3 different numbers, we can use this prinicple:
gcd(a, b, c) = gcd( a, gcd(b, c) )
So we apply the Euclidean algorithm twice. Let's see if this works!
gcd(9118, 12173, 33182) = gcd( 9118, gcd(12173, 33182) )
First, use the Euclidean algorithm to find the inner piece.
= gcd(12173, 33182)
= gcd(12173, 21009)
= gcd(12173, 8836)
= gcd(3337, 8836)
= gcd(3337, 5499)
= gcd(3337, 2162)
= gcd(1175, 2162)
= gcd(1175, 987)
= gcd(188, 987)
= gcd(188, 799)
= gcd(188, 611)
= gcd(188, 423)
= gcd(188, 235)
= gcd(188, 47)
= gcd(141, 47)
= gcd(94, 47)
= gcd(47, 47)
= 47
Next, use the Euclidean algorithm to find the outer piece.
gcd( 9118, gcd(12173, 33182) )
= gcd(9118, 47)
= gcd(9071, 47)
= gcd(9024, 47)
.
. *Note that 9118 - 47*193 = 47 so we would have to subtract 47 a total of 193 times.*
.
= gcd(141, 47)
= gcd(94, 47)
= gcd(47, 47)
= 47
This agrees with Melody's answer!!
We put one open curly brace beside the "pieces" of the piecewise function, for example:
\(f(x)=\begin{cases} x+2 & \text{if}&x> 2 \\ x^2 &\text{if}& -3< x\leq 2 \\ 9 &\text{if}& x\leq-3 \end{cases}\)
This is the way to show the pieces of a piecewise function.
On the other hand, domains and ranges (and, of course, intervals) can be expressed in interval notation.
An interval is a set of values or numbers - not a set of expressions or functions.
E.g., the interval [0, 5) is every number between 0 and 5, including 0 and excluding 5.
And by looking at the graph for this function:
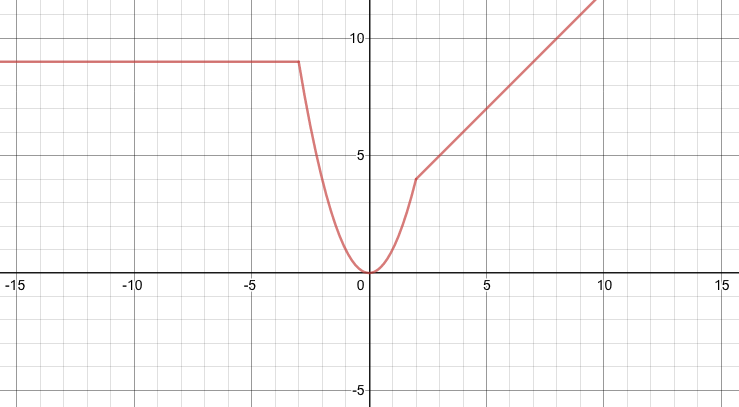
We can see:
| The domain is: | _ | (-∞, ∞) | ||
| The range is: |
| [0, ∞) | ||
| The intervals of decrease are: | (-3, 0) | ← | This means the function is decreasing for all x values in the interval (-3, 0) For instance, when x = -1, the function is decreasing. | |
| The intervals of increase are: |
| (0, 2) and (2, ∞) |
All of those are intervals expressed in interval notation.
(At the points where x = 2 and x = -3 , the slope is undefined, and so the function is neither increasing nor decreasing, and so we do not include those values in the intervals of increase or decrease.)
If the graph passes the vertical line test, then it is a function.
Here are a bunch of examples: https://imgur.com/a/Px4lYIt
(If you still are wondering about whether a particular situation is considered a function or not, you could try to draw it on desmos and share the graph or draw it on a piece of paper and take a photo.)
Also, you might want to read the first paragraph of this page: https://en.wikipedia.org/wiki/Interval_(mathematics)
Hope this helps somewhat! If you're confused about something, please say so! ![]()
f(x) = x h(x) = 13x + 1
By the transitive property of equality,
f(x) = 13x + 1
Here is the graph of f: https://www.desmos.com/calculator/gmr9uc3oer
x h(x) = 13x + 1 Divide both sides of this equation by x
h(x) = 13 + 1/x
Here is the graph of h: https://www.desmos.com/calculator/bbndyocwqm
*edit* Now I realize this answer is probably totally wrong, but I will leave it anyway...LOL
We are given that f(11) = 34 so we know that 11 is in the domain.
domain so far = {11}
There exists an integer 11 such that f(11) = 34 , so f(34) is defined. And so 34 is in the domain.
domain so far = {11, 34}
So notice that just like we had to add the result of f(11) to the domain, we will now have to add the result of f(34) to the domain (then the result of that, and the result of that, etc.).
| f(34) = 17 | _____ | domain so far = {11, 34, 17} |
| f(17) = 52 |
| domain so far = {11, 34, 17, 52} |
| f(52) = 26 | domain so far = {11, 34, 17, 52, 26} | |
| f(26) = 13 |
| domain so far = {11, 34, 17, 52, 26, 13} |
| f(13) = 40 | domain so far = {11, 34, 17, 52, 26, 13, 40} | |
| f(40) = 20 |
| domain so far = {11, 34, 17, 52, 26, 13, 40, 20} |
| f(20) = 10 | domain so far = {11, 34, 17, 52, 26, 13, 40, 20, 10} | |
| f(10) = 5 |
| domain so far = {11, 34, 17, 52, 26, 13, 40, 20, 10, 5} |
| f(5) = 16 | domain so far = {11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16} | |
| f(16) = 8 |
| domain so far = {11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8} |
| f(8) = 4 | domain so far = {11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4} | |
| f(4) = 2 |
| domain so far = {11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2} |
| f(2) = 1 | domain so far = {11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1} | |
| f(1) = 4 |
| domain so far = {11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1} |
Finally, we have reached a point where we do not have to add anything else to the domain.
4 is already in the set, so we do not have to add anything else.
So the smallest possible number of integers in the domain is 15
(Thank you CPhill for correcting my previous mistake!)