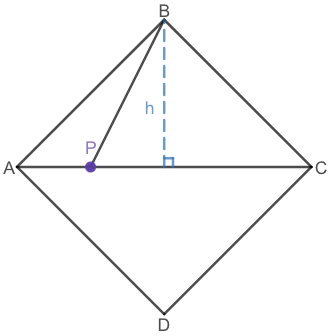
See: https://www.desmos.com/calculator/sln5zuurfx
We know that
AP / PC = 1 / 3
We are also given that AP = 10 so we can substitute 10 in for AP
10 / PC = 1 / 3
If it isn't already clear that PC must be 30 , we can invert both sides
PC / 10 = 3 / 1
and then multiply both sides of the equation by 10
PC = 3 / 1 * 10
PC = 30
And now we can find the length of AC
AC = AP + PC = 10 + 30 = 40
The diagonals of a square are the same length and bisect each other so...
h = AC / 2 = 40 / 2 = 20 where h is the height of triangle BPC
Area of triangle BPC = ( 1/2 )( PC )( h ) = ( 1/2 )( 30 )( 20 ) sq units = 300 sq units