ElectricPavlov

Close., but not quite correct ... it is   \(x =\sqrt{3}\)  / 2   

Find unit cost per inch 

48 cents / 12 inches =   4 cents/ inch

now for 39 inches 

     39 inches * 4 cents/ inch = 156 cents     ( $ 1.56) 

t = 2   hrs 

A = 145 - 25 = 120

Te =  25 

T(t) = 70 =  120 e^(k *2) + 25     solve for k = - . 49041

T(t) = 120 e^(- .49041 t )   + 25 

  40 = 120 e^(-.49041 t) + 25          solve  for t = 4. 24 hours 

( Let me know if this is incoorrect and I will re-evaluate) 

g = grogg now     d = dad 

(g-7)  * 8   = (d-7)        8g - 56 = d-7         8g =  d + 49    <======given

(g-3) *5  = d- 3          5g-15 = d-3             5g = d + 12             Subtract bottom equation from top 

                                                                  3g = 37 

                                                                     g = 12 1/3   y/o         then   d  = 8g - 49 =  49 2/3 y/o   <====dad's age now 

Zero chance   ....if there are  three pieces and they are all less than two inches....that is less than the original 6 inch total length. 

3/8   is notation for    3 ÷ 8     if you use tour calculator , you will find = .375 

Not sure what the question is ....but 

x^2 -12   =   ( x- sqrt12)(x+sqrt 12)            

Are you familiar with the order guidelines used complete calculations of equations called PEDMAS ? 
parentheses  first

exponents    next 

division/multiplication next 

addition/subtraction next

  using these rules 

-2 + 1^2       do the exponent firist     -2 +1     now do the addition   = -1 

(-2+1)^2      do the parentheses first   -1 ^2    now do the exponent   = 1 

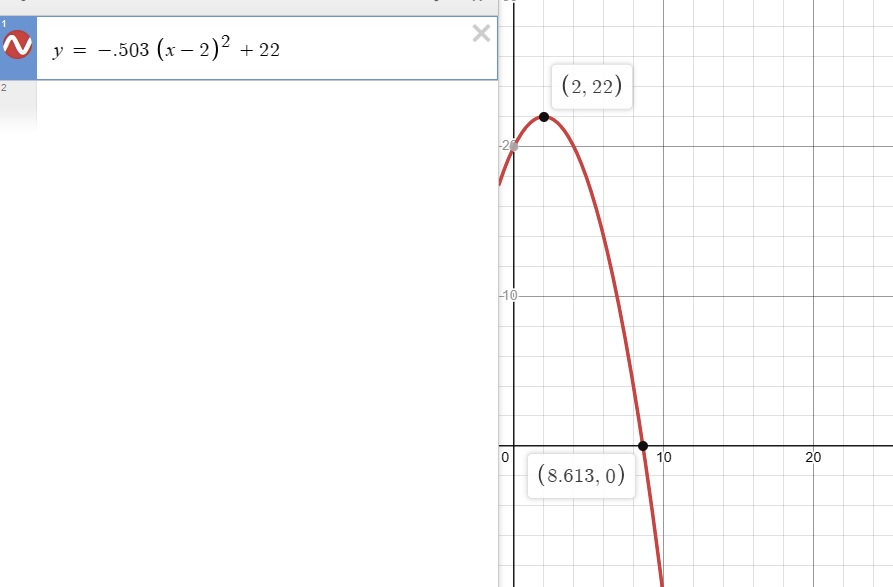
Parabola with vertex at 2, 22

Find her initial vertical speed  (she only goes up 2 feet against gravity) 

         vf = 0 = v0 +  at        a =  - 32.2 ft/s^2 

                0 = vo  - 32.1 t       shows vo = 32.1 t

then    d = do + vo t  - 16.1 t^2   <=====  Use this to find 't' 

        22 = 20 +  (32.1 t) ^t  - 16.1 t^2 

            2 = 16.1 t^2 

             t = .3525 seconds             her horizontal speed is then 2 ft / .3525 s = 5.675 f/s    and vertical speed is 32.1 * .3525 = 11.31 f/s

Find a point on the parabola 

            at    t = 1 sec     x = 5.675 ft    and y =   d = do + vo t + 1/2 at^2 = 20 + 11.31(1) - 16.1 (1^2) =  15.21 ft

vertex form of the parabola 

     y = a ( x-2)^2 + 22           and when x = 5.675   y = 15.21 

                    shows a = -.503 

a)  Trajectory equation becomes     y = -.503 (x-2)^2  + 22    

b) when she hits the water y = 0  = -.503 ( x-2)^2 + 22      shows x = 8.6 ft 

Here is a graph that shows this:

27^2   +   2/3 * 27 * 2/3 * 27      + .......

=    27^2   +  (2/3 * 27)^2      +   (2/3)^4 * 27^2     + (2/3)^6  27^2   + (2/3)^8 * 27^2    =

(2/3^0  + 2/3 ^2  + 2/3 ^4 + 2/3 ^6 )  * 27^2    =   1289  4/9  units^2

Double check:

27^2   + 18^2   + 12^2   + 8^2   + (5 1/3)2  = 1289 4/9     <===CHECK !