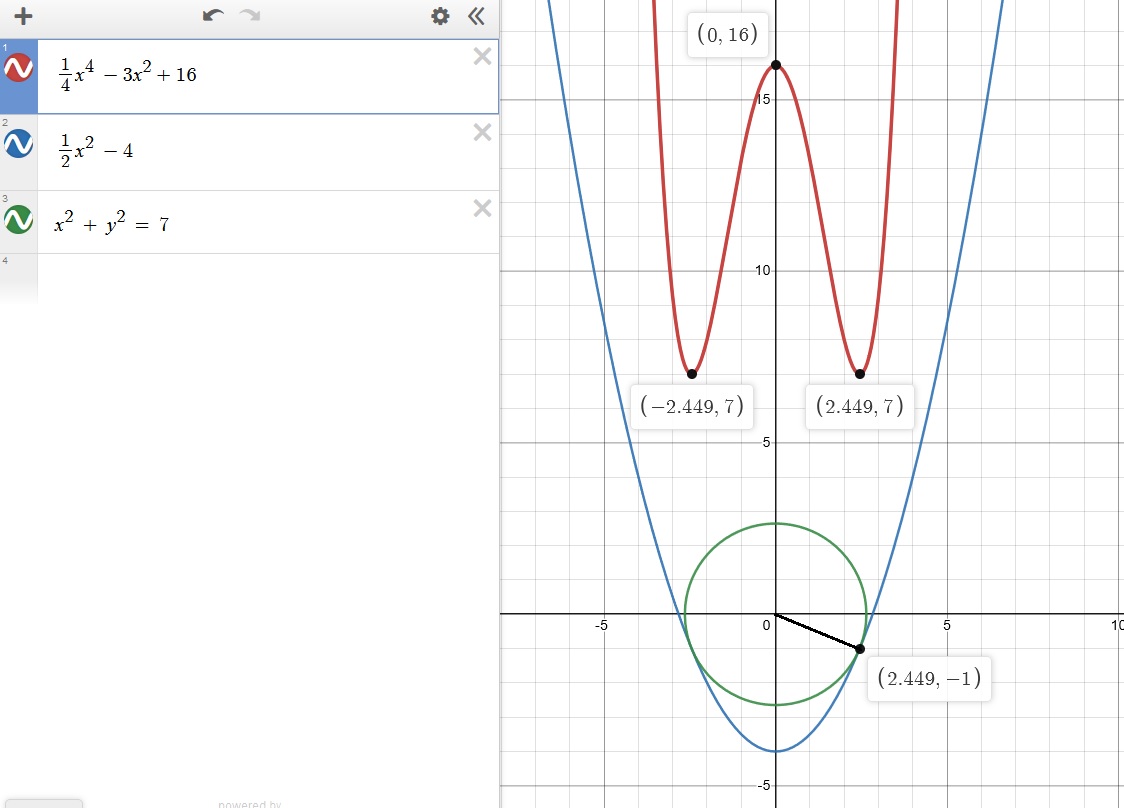
Use the distance formula to find the disatnce from the point (x,y) to the origin....where y = -1/2x^2 - 4
d^2 = (x-0)^2 + ( -1/2 x^2 -4 -0)^2
= 1/4 x^4 -3x^2 + 16
Now take the derivative and set = 0 to find the local maxima/minma points ( this is where the graph of the function has a slope = 0)
x^3 -6x = 0
x ( x^2 -6) = 0 shows the 'x' coordinate possibilities to be ± √6 and 0 BUT we need to jnow if these points are maxima or minima
...... to determine this, take the derivative AGAIN
3x - 6 now sub in the found 'x' values .... a positive result means the 'x' point is a minima
when x = 0 the value is -6 <==== this would be a maxima
when x = ± √6 the result is positive <==== so either of these 'x' s are the coordinte for the nearest point
find the 'y' coordinate by sustituting in the 'x ' into the original equation to find y = - 1
so the nearest point would be ( √6 , -1)
Here is a graph to SEE this :