In order to find the mean, find the sum of all the data points and divide by the number of data points. Since this is a "lunch expenditure for a week," I would assume that this is only a sample, so I will x bar as the mean.
\(\overline{x}=\frac{4.85+5.10+5.50+4.75+4.50+5.00+6.00}{7}=$5.10\)
Yet again, I am making the assumption that this data is a sample because that seems like a reasonable assumption. In order to find the standard deviation, this formula will provide that answer:
\( \text{SD}_{\text{sample}}=\sqrt{\frac{\Sigma_{i=1}^{n} (x_{i}-\overline{x})^2}{n-1}}\)
Now, this is a loaded formula! Let's first define a few variables:
\(x_i\) is the individual data point
\(\overline{x}\) is the average of the data set
\(n\) is the number of data points
Let's break this formula down. There are 5 steps, one of which we have already done.
I will show the work with a table. This takes care of steps 2 and 3 simultaneously.
| Day | \(x_i\) | \(x_i-\overline{x}\) | \((x_i-\overline{x})^2\) | ||
| Monday | 4.85 | -0.25 | 0.0625 | ||
| Tuesday | 5.10 | 0.00 | 0.0000 | ||
| Wednesday | 5.50 | 0.40 | 0.1600 | ||
| Thursday | 4.75 | -0.35 | 0.1225 | ||
| Friday | 4.50 | -0.60 | 0.3600 | ||
| Saturday | 5.00 | -0.10 | 0.0100 | ||
| Sunday | 6.00 | 0.90 | 0.8100 | ||
| Total | 1.5250 | ||||
Now, I will do the remaining steps.
\(\text{SD}_{\text{sample}}\sqrt{\frac{1.525}{7-1}}\approx0.504\)
The variance is just the square of the standard deviation.
\(\text{S}^2=\left(\sqrt{\frac{1.525}{6}}\right)^2=\frac{1.525}{6}\approx0.2542\)
19) Picking a random number, say 2932, is independent to a coin flip; one has no effect on the other.
Geometers detest making assumptions; it is generally frowned upon because the idea to construct sound logic using previous theorems and postulate to formulate new ideas. However, rectangles cannot have lengths--sides can. Because of this, I have had to dissect the given information and have had to make an educated guess as to where the given information fits. I will let this diagram demonstrate this:
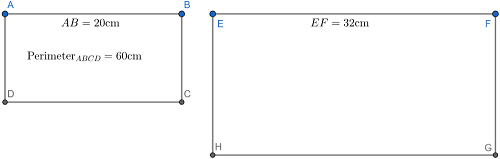
We can solve for the remaining side length, \(BC\), by understanding the perimeter formula for a rectange.
| \(2(AB+BC)=\text{Perimeter}_{ABCD}\) | Let's plug in the known values and solve for the missing one. |
| \(2(20\text{cm}+BC)=60\text{cm}\) | Instead of distributig the 2, we can divide it from both sides. |
| \(20\text{cm}+BC=30\text{cm}\) | Subtract 20cm from both sides to finish the algebra. |
| \(BC=10\text{cm}\) | |
We know that \(EFGH\) is similar to \(ABCD\), which means that the sides are proportional. We can use this information to our advantage.
| \(\frac{AB}{BC}=\frac{EF}{FG}\) | Yet again, substitute in the known values and solve for the unknown. |
| \(\frac{20\text{cm}}{10\text{cm}}=\frac{32\text{cm}}{FG}\) | Let's simplify the left hand side of this proportion so that the calculation is easier. |
| \(2=\frac{32\text{cm}}{FG}\) | We can use cross-multiplication here to clear all fractions. |
| \(2FG=32\text{cm}\) | Divide by 2 from both sides. |
| \(FG=16\text{cm}\) | We are not done yet! We must find the area of the rectange. That's what the question is asking for, after all! |
| \(\text{Area}_{EFGH}=EF\cdot FG\) | Plug those values in. |
| \(\text{Area}_{EFGH}=32\text{cm}*16\text{cm}=512\text{cm}^2\) | This is your final answer! |
59. This is a very specific case where we can use this relationship, but it turns out that the hypotenuse of \(\triangle PRQ\) can be calculated using the geometric mean of the individual segments \(\overline{PS}\text{ and }\overline{SQ}\). The geometric mean is the nth root of the product of n numbers. In other words,
| \(RS=\sqrt{PS\cdot SQ}\) | We know the length of both of these, so we can solve for the missing length. |
| \(RS=\sqrt{4*16}\) | Now, simplify. |
| \(RS=\sqrt{64}=8\) | In the context of geometry where lengths are involved, only the positive answer is ever considered. |
We can find the other lengths using the Pythagorean's Theorem.
| \(PS^2+SR^2=RP^2\) | Plug in the values we know and solve for the unknown. |
| \(4^2+8^2=RP^2\) | |
| \(16+64=RP^2\) | |
| \(80=RP^2\) | Take the square root of both sides and reject the negative answer. |
| \(RP=\sqrt{80}=4\sqrt{5}\approx8.9 \) | |
| \(QS^2+SR^2=RQ^2\) | Do the same process as before to solve for the missing length. |
| \(16^2+8^2=RQ^2\) | This is now a matter of simplification. |
| \(256+64=RQ^2\) | |
| \(320=RQ^2\) | Take the principal root of both sides. |
| \(RQ=\sqrt{320}=8\sqrt{5}\approx17.9\) | |
Note to CPhill: Your ratio was close. It should have been \(\frac{RQ}{PR}=\frac{SQ}{RS}\). Visually, it is tricky to determine similar side lengths, which is why I generally avoid them. The similarity statement should be \(\triangle PRQ\sim \triangle PSR\sim \triangle RSQ\).
I think I have a way of figuring out this problem. It may not be the most efficient, but it gets the problem done.
Both ranging from 1 to 10, "x" and "y" are two numbers, and their product plus one equals the the number your friend got. I can create an equation with this.
| \(xy+1=(x-4)(2y-1)\) | I am going to solve for y and see if I can make any more observations. First, let's expand. |
| \(xy+1=2xy-x-8y+4\) | In order to solve for y, move every term with a "y" to one side. |
| \(8y-xy=3-x\) | Let's factor out a "y" since that is the GCF of the left hand side of the equation. |
| \(y(8-x)=3-x\) | Divide by 8-x to isolate y completely. |
| \(y=\frac{3-x}{8-x}, x\neq 8\) | We can now begin to guess x-values and hope they output integers in between 1 to 10 for y. |
Now, I will not guess that is 4 or below because that would result my friend's corresponding x-value to be negative, and that can never be one more than my product. Let's start guessing at 5 to 10.
\(\frac{3-5}{8-5}=\frac{-2}{3}\\ \frac{3-6}{8-6}=\frac{-3}{2}\\ \frac{3-7}{8-7}=\frac{-4}{1}=-4\\ \frac{3-9}{8-9}=\frac{-6}{-1}=6\\ \frac{3-10}{8-10}=\frac{-7}{-2}\)
Look at that! A match has appeaed! x=9 and y=6. That's the only solution, too.
When x=9 and y=6, the product of my numbers is 54.