a) We could use the Law of Cosines to find θ , but since △ABC is an isosceles triangle, we can split it into two
congruent right triangles by drawing a height from C to side AB, like this:
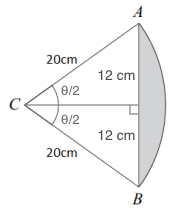
| sin( angle ) = opposite / hypotenuse | |
| sin( θ/2 ) = 12 / 20 |
|
| θ/2 = arcsin( 12/20 ) | |
| θ = 2arcsin( 12/20 ) |
|
| θ ≈ 1.287 |
b) arc length = (radius) * (angle measured in radians) ≈ (20 cm) * (1.287) ≈ 26 cm
c)
i) sector area = (angle measured in radians)/2 * (radius)2 ≈ (1.287)/2 * (20)2 cm2 ≈ 257.4 cm2
ii) shaded area = sector area - triangle area ...Do you know how to find the area of the triangle?
It appears there are four "zero-width space" characters in your LaTeX code. Two of them are between the 3/4 and the x which is why it doesn't look normal. I found that out by pasting your code into this website: https://www.soscisurvey.de/tools/view-chars.php
----------
As for your actual question, this is pretty much the method guest used:
\(\frac34x+\frac58=4x\)
And \(\frac34x=\frac{3x}{4}\) so we can rewrite it like this...
\(\frac{3x}{4}+\frac58=4x\)
To get a common denominator, we can multiply \(\frac{3x}4\) by \(\frac22\) which won't change its value.
\(\frac22\cdot\frac{3x}4+\frac58=4x\)
And \(\frac22\cdot\frac{3x}4=\frac{6x}8\) ←That's how it went from 3x to 6x
\(\frac{6x}8+\frac58=4x\)
Now that the fractions have a common denominator we can combine them.
\(\frac{6x+5}{8}=4x\)
Multiply both sides of the equation by 8
\(6x+5=32x\)
Subtract 6x from both sides.
\(5=32x-6x\)
\(5=26x\)
Divide both sides by 26
\(\frac5{26}=x\)
----------
Also, we could multiply both sides of the equation by 8 to begin with, like this:
\(\frac34x+\frac58\ =\ 4x\\~\\ 8\big(\frac34x+\frac58\big)\ =\ 8\big(4x\big)\\~\\ 8\cdot\frac34\cdot x\ +\ 8\cdot\frac58\ =\ 8\cdot4\cdot x\\~\\ 6x\ +\ 5\ =\ 32x\\~\\ 5\ =\ 26x\\~\\ \frac{5}{26}\ =\ x\)_