hairyberry

Because $P_1P_2P_3\dots {P}_{10}$is a regular polygon, all the side lengths are equal.

Therefore we only need to calculate ${(\overline{P_1P_2)}}^{2}*10$.

Suppose the center of the circle is O, then $\angle P_1OP_2 = {36}^{\circ}$.

Apply law of cosines:

${(\overline{P_1P_2)}}^{2}={1}^{2}+{1}^{2}-2*\frac{\sqrt{5}+1}{4}=2-\frac{\sqrt{5}+1}{2}$.

${(\overline{P_1P_2)}}^{2}*10=20-10(\frac{\sqrt{5}+1}{2})=20-5\sqrt{5}-5=15-5\sqrt{5}$.

So our answer is $15-5\sqrt{5}$.

1)

To simplify this equation, we want to eliminate some of the terms. Set 

$x=a_1-a_2$

$y=a_2-a_3$

Therefore:

$a_3-a_1=-(a_1-a_3)=-(x+y)=-x-y$.

Now our equation is:

$|x|+2|y|+3|-x-y|=1$. 

$|x|+2|y|+3|x+y|=1$.

One way to approach this is by graphing. 

We split this into 3 sections:

One for $x \ge 0, x < 0$

$y\ge0, y<0$

For $|x+y|$ we have

$x>-y, x < -y$.

Here is a graph, with $x=0, y=0, x=-y$ labeled. (The green one is $|x|+2|y|+3|x+y|=1$).

We see the largest possible value of $|x|$ in this graph is $\frac{1}{3}$.

Therefore, the maximum value is $|a_1-a_2|=\frac{1}{3}$.

A period is the distance between each repetition.
It's easy to see that after 12, f(m) starts repeating again.

Therefore the period is 12.

The vertical shift of this function is how much it's shifted up.

The sine function started at 50, so the vertical shift is 50 (also it's easy to see 50 is the midpoint).

Because 3 is right in between 0 and 6, it is the max value, similarly 9 is the min value.

So 50-33 = 17, and 67-50 = 17 too, so the amplitude is 17.

Therefore, The amplitude of the sine function is 17. The period of the sine function is 12. The vertical shift of the function is 50.

If it interests you, the equation of the function is $f(m)=-17\sin(\frac{2\pi}{12}m)+50$.

The function inside, $f(x) = \left\lfloor\frac{2 - 3x}{3x + 1}\right\rfloor$ is $\frac{2-3x}{3x+1}$.

Using what we know about rational functions, set the inside function,  to g(x), $g(x) = \frac{2-3x}{3x+1}$ has a x intercept of 2/3, and a horizontal asymptote of -1, and a vertical asymptote at x = -1/3.

Using this information, we can determine the relative shape of the graph.

Because the function has an x intercept at 2/3, and the function only goes down after that, but will not go down past -1, since that is our horizontal asymptote. Plugging in values from $1\le x \le \infty$ will always result in a output of $-1\le g(x) \le 0$.

Therefore because $f(x)=\lfloor\frac{2-3x}{3x+1}\rfloor$, if x is from 1 to 1000 will always result in -1.

Therefore $f(1)+f(2)+f(3) + \dots + f(999) + f(1000) = -1000$.

The period is the distance between any repetition of the function. In the sinusoidal curve, this is usually the distance between every two times it passes the midline.

It's easy to see that from 0-2 the function curves up, from 2-4 the function curves down, then back up from 4-6 etc. 

Therefore the period is 4.

From the start, we know the porportion of the amount of water in the beaker, to the total amount of solution in the beaker.

The amount of acid drained away to the amount of water drained away is in porportion to their original amounts.

We know $\frac{150}{200+800}$of the total amount is drained away, so $200*\frac{150}{200+800}=30$.

So there is $200-30=170$mL left.

Adding 150mL water gives 320mL water.

We know that the total amount of solution didn't change, so there is $1000-320=680$mL acid.

Similarly, now $320*\frac{150}{320+680}=48$ mL drained away.

Subtracting this, and adding the 150 mL of water, we have 422mL of water now.

${(3+\sqrt{5})}^{2}*{(2-\sqrt{5})}^{7}$

Simplify the left side first:

${(3+\sqrt{5})}^{2}=14+6\sqrt{5}$

Split some terms apart to find the right side.

$(2-\sqrt{5})^{2}=9-4\sqrt{5}$

${(2-\sqrt{5})}^{4}={(9-4\sqrt{5})}^{2}=161-72\sqrt{5}$

${(2-\sqrt{5})}^{7}={(2-\sqrt{5})}^{4}*{(2-\sqrt{5})}^{2}*{(2-\sqrt{5})}$.

$=(161-72\sqrt{5})(9-4\sqrt{5})(2-\sqrt{5})=12238-5473\sqrt{5}$

With a little help from calculators, this is 

$(14+6\sqrt{5})*(12238-5473\sqrt{5})=7142-3194\sqrt{5}$.

There is color A and Color B.

Either there is:

3 sides color A 0 sides color B

3 sides color B 0 sides color A

2 sides color A 1 side color B

1 side color B 2 sides color A

Each of these has exactly one way of occuring, because they can always be rotated back to the same position

So there are 4 colorings. 

This formula 

$\cos(x)=\frac{a\cdot b}{||a||\,||b||}$. Just to clarify, The $\cdot$ between the a and b is not a multiplication sign, it is a dot product.

This formula is very useful for calculating the angle between 2 vectors.

To prove: draw a vector, connecting vector  $\vec{a}$ and $\vec{b}$, remembering vector subtraction, this vector is $\vec{a-b}$.

We see a cosine, so we hope to use the law of cosines to help us relate side lengths. However, we don't know the side lengths of these vectors. However, we have a very important symbol called the norm, $||~||$, and this the distance to the endpoint to the origin. Remember, vectors aren't defined with position, so norm gives an effective way to represent length. Here is a graph:

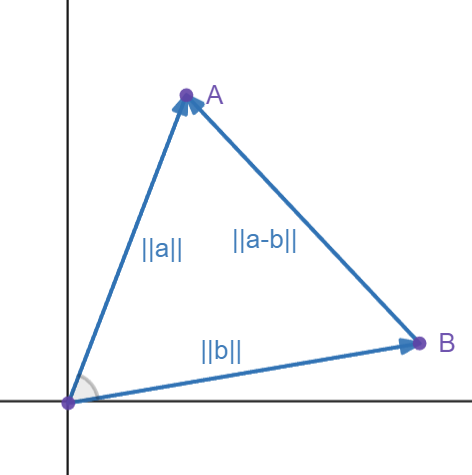
Set $\theta = \angle AOB$

Therefore by the law of cosines, we have:

$\cos(\theta) = \frac{{||a||}^{2}+{||b||}^{2}-{||a-b||}^{2}}{2||a||\,||b||}$.

To relate norm to dot product, we have another very important formula:

$v\cdot v ={||v||}^{2}$. (dot product again). PS, notice the resemblance to the formula $z*\overline{z}={|z|}^{2}$, for complex number z.

Using this formula, 

$\cos(\theta) = \frac{a\cdot a+b\cdot b-(a-b)\cdot(a-b)}{2||a||\,||b||}$.

Dot products have a special property, because they are commutative, and distributive.

Therefore, $\cos(\theta) = \frac{a\cdot a+b\cdot b-(a\cdot a- 2a\cdot b + b\cdot b)}{2||a||\,||b||}$

Simplifying:

$\cos(\theta) = \frac{2a \cdot b}{2||a|| \, ||b||}=\frac{a\cdot b}{||a||\,||b||}$.

This gives our desired formula.

Set the distance to d, and the speed of the plane as x.

When there is no wind using the formula, distance/rate = speed.

$\frac{2d}{x}=\frac{27}{4}$.

When there is wind on our war there we are 50 mph faster, but on our way back we are 50 mph slower, so

$\frac{d}{x+50}+\frac{d}{x-50}=\frac{15}{2}$.

$\begin{cases}\frac{2d}{x}=\frac{27}{4}\\\frac{d}{x+50}+\frac{d}{x-50}=\frac{15}{2}\end{cases}$

$\begin{cases}d=\frac{27}{8}x \\ \frac{d}{x+50}+\frac{d}{x-50}=\frac{15}{2} \end{cases}$

$\frac{27x}{4x+200}+\frac{27x}{4x-200}=15$

We get our positive answer is $x=50\sqrt{10}$, note the negative answer is $-50\sqrt{10}$, which is the same because it just means the wind is blowing in the opposite direction.

Therefore,  $\bf{d = 50\sqrt{10}*\frac{27}{8}=\frac{675}{4}\sqrt{10}}$.